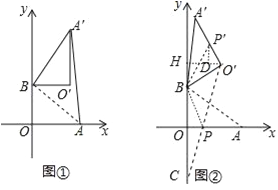
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转,得△A′BO′,点A,O旋转后的对应点为A′,O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)在(2)的条件下,边OA上 的一点P旋转后的对应点为P′,当O′P+BP′取得最小值时,求点P′的坐标(直接写出结果即可)

参考答案:
【答案】(1)、5![]() ;(2)、(
;(2)、(![]() );(3)、(
);(3)、(![]() ,
,![]() )
)
【解析】试题分析:(1)、如图①,先利用勾股定理计算出AB=5,再根据旋转的性质得BA=BA′,∠ABA′=90°,则可判定△ABA′为等腰直角三角形,然后根据等腰直角三角形的性质求AA′的长;(2)、作O′H⊥y轴于H,如图②,利用旋转的性质得BO=BO′=3,∠OBO′=120°,则∠HBO′=60°,再在Rt△BHO′中利用含30度的直角三角形三边的关系可计算出BH和O′H的长,然后利用坐标的表示方法写出O′点的坐标;(3)、由旋转的性质得BP=BP′,则O′P+BP′=O′P+BP,作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,易得O′P+BP=O′C,利用两点之间线段最短可判断此时O′P+BP的值最小,接着利用待定系数法求出直线O′C的解析式为y=![]() x﹣3,从而得到P(
x﹣3,从而得到P(![]() ,0),则O′P′=OP=
,0),则O′P′=OP=![]() ,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
,作P′D⊥O′H于D,然后确定∠DP′O′=30°后利用含30度的直角三角形三边的关系可计算出P′D和DO′的长,从而可得到P′点的坐标.
试题解析:(1)、如图①, ∵点A(4,0),点B(0,3), ∴OA=4,OB=3, ∴AB=![]() =5,
=5,
∵△ABO绕点B逆时针旋转90°,得△A′BO′, ∴BA=BA′,∠ABA′=90°,
∴△ABA′为等腰直角三角形, ∴AA′=![]() BA=5
BA=5![]() ;
;
(2)、作O′H⊥y轴于H,如图②, ∵△ABO绕点B逆时针旋转120°,得△A′BO′,
∴BO=BO′=3,∠OBO′=120°, ∴∠HBO′=60°, 在Rt△BHO′中,∵∠BO′H=90°﹣∠HBO′=30°,
∴BH=![]() BO′=
BO′=![]() ,O′H=
,O′H=![]() BH=
BH=![]() , ∴OH=OB+BH=3+
, ∴OH=OB+BH=3+![]() , ∴O′点的坐标为(
, ∴O′点的坐标为(![]() );
);
(3)∵△ABO绕点B逆时针旋转120°,得△A′BO′,点P的对应点为P′, ∴BP=BP′,
∴O′P+BP′=O′P+BP, 作B点关于x轴的对称点C,连结O′C交x轴于P点,如图②,
则O′P+BP=O′P+PC=O′C,此时O′P+BP的值最小, ∵点C与点B关于x轴对称, ∴C(0,﹣3),
设直线O′C的解析式为y=kx+b,
把O′(![]() ),C(0,﹣3)代入得
),C(0,﹣3)代入得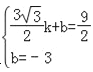 ,解得
,解得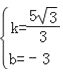 ,
,
∴直线O′C的解析式为y=![]() x﹣3, 当y=0时,
x﹣3, 当y=0时,![]() x﹣3=0,解得x=
x﹣3=0,解得x=![]() ,则P(
,则P(![]() ,0),
,0),
∴OP=![]() , ∴O′P′=OP=
, ∴O′P′=OP=![]() , 作P′D⊥O′H于D,
, 作P′D⊥O′H于D,
∵∠BO′A=∠BOA=90°,∠BO′H=30°, ∴∠DP′O′=30°,
∴O′D=![]() O′P′=
O′P′=![]() ,P′D=
,P′D=![]() , ∴DH=O′H﹣O′
, ∴DH=O′H﹣O′![]() ,
,
∴P′点的坐标为(![]() ,).
,).
-
科目: 来源: 题型:
查看答案和解析>>【题目】菏泽牡丹机场位于菏泽市定陶区孟海镇西北,距満泽市中心直线距离约20公里,飞行区指标为4C级,跑道长2600米,菏泽机场性质为国内支线机场,计划2019年10月1日建成通航,预计机场年旅客吞吐量900000人次.数据900000用科学记数法表示为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
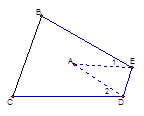
A.∠A=∠1+∠2
B.2∠A=∠1+∠2
C.3∠A=2∠1+∠2
D.3∠A=2(∠1+∠2) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,BE平分∠ABC,CF平分∠BCD,BE、CF交于点G.若使EF=
 AD,那么平行四边形ABCD应满足的条件是( )
AD,那么平行四边形ABCD应满足的条件是( ) 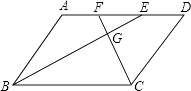
A.∠ABC=60°
B.AB:BC=1:4
C.AB:BC=5:2
D.AB:BC=5:8 -
科目: 来源: 题型:
查看答案和解析>>【题目】若x2+2(m﹣1)x+36是完全平方式,则m=__.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若a>b,则-9a________-9b.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣3x+m=0的一个根是1,则m= , 另一个根为 .
相关试题

