【题目】如图在平面直角坐标系xOy中,反比例函数y1= ![]() (x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).
(x>0)的图象与一次函数y2=kx-k的图象的交点为A(m,2).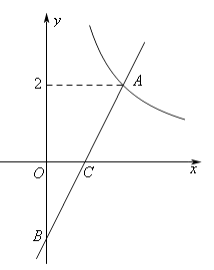
(1)求一次函数的解析式;
(2)观察图像,直接写出使y1≥y2的x的取值范围.
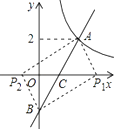
(3)设一次函数y=kx-k的图象与y轴交于点B,若点P是x轴上一点,且满足△PAB的面积是4,请写出点P的坐标.
参考答案:
【答案】
(1)解:将A(m,2)代入 ![]() (x>0)得,m=2,则A点坐标为A(2,2),将A(2,2)代入y=kx-k得,2k-k=2,解得k=2,则一次函数解析式为y=2x-2
(x>0)得,m=2,则A点坐标为A(2,2),将A(2,2)代入y=kx-k得,2k-k=2,解得k=2,则一次函数解析式为y=2x-2
(2)解:当0<x≤2时, y1≥y2 ;
(3)解:∵一次函数y=2x-2与x轴的交点为C(1,0),与y轴的交点为B(0,-2),S△ABP=S△ACP+S△BPC,
∴ ![]() ×2CP+
×2CP+ ![]() ×2CP=4,解得CP=2,则P点坐标为(3,0),(-1,0)
×2CP=4,解得CP=2,则P点坐标为(3,0),(-1,0)
【解析】(1)首先把A点的坐标代入反比例函数的解析式求出A点的坐标,再把A点的坐标代入一次函数的解析式求出k的值,从而得出一次函数的解析式;
(2)利用图像求不等式的解集,就是弄清谁大谁小,谁大就看谁的图像在上方的时候的自变量的取值范围;
(3)求出一次函数y=2x-2与x轴的交点C的坐标,与y轴的交点B的坐标,利用S△ABP=S△ACP+S△BPC,列出方程求出CP的长,从而得到P点的坐标。
【考点精析】认真审题,首先需要了解确定一次函数的表达式(确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法).
-
科目: 来源: 题型:
查看答案和解析>>【题目】若二次函数y=-2x2+bx+c的顶点坐标为(2,-3),则此函数有( )
A.最大值2
B.最大值-3
C.最小值2
D.最小值-3 -
科目: 来源: 题型:
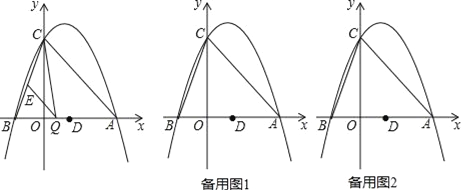
查看答案和解析>>【题目】如图,抛物线y=ax2﹣2ax+c(a≠0)与y轴交于点C(0,4),与x轴交于点A、B,点A坐标为(4,0).
(1)求该抛物线的解析式;
(2)抛物线的顶点为N,在x轴上找一点K,使CK+KN最小,并求出点K的坐标;
(3)点Q是线段AB上的动点,过点Q作QE∥AC,交BC于点E,连接CQ.当△CQE的面积最大时,求点Q的坐标;
(4)若平行于x轴的动直线l与该抛物线交于点P,与直线AC交于点F,点D的坐标为(2,0).问:是否存在这样的直线l,使得△ODF是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
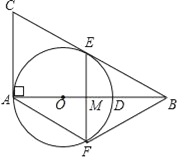
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,O是AB边上的一点,以OA为半径的⊙O与边BC相切于点E.
(1)若AC=6,BC=10,求⊙O的半径.
(2)过点E作弦EF⊥AB于M,连接AF,若∠AFE=2∠ABC,求证:四边形ACEF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个三角形三个内角度数的比为1︰2︰3,那么这个三角形是( )
A.直角三角形 B.锐角三角形 C.钝角三角形 D.等边三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的半径为5厘米,当OP=6厘米时,点P在⊙O . (填“内”或“外”或“上”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】若xn=4,yn=9,则(xy)n=________.
相关试题

