【题目】如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1500m,小敏行走的路线为B→A→G→E,小聪得行走的路线为B→A→D→E→F.若小敏行走的路程为3100m,则小聪行走的路程为m.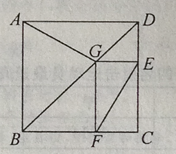
参考答案:
【答案】4600
【解析】解:小敏走的路程为AB+AG+GE=1500+(AG+GE)=3100,
则AG+GE=1600m,
小聪走的路程为BA+AD+DE+EF=3000+(DE+EF).
连接CG,
在正方形ABCD中,∠ADG=∠CDG=45°,AD=CD,
在△ADG和△CDG中,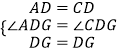
所以△ADG△CDG,
所以AG=CG.
又因为GE⊥CD,GF⊥BC,∠BCD=90°,
所以四边形GECF是矩形,
所以CG=EF.
又因为∠CDG=45°,
所以DE=GE,
所以小聪走的路程为BA+AD+DE+EF=3000+(GE+AG)=3000+1600=4600(m).
所以答案是4600.
【考点精析】关于本题考查的正方形的性质,需要了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形EFGH四个顶点分别在菱形ABCD的四条边上,BE=BF,将△AEH,△CFG分别沿边EH,FG折叠,当重叠部分为菱形且面积是菱形ABCD面积的
 时,则
时,则  为( )
为( )
A.
B.2
C.
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y=
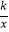 (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 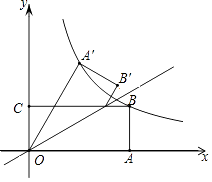
-
科目: 来源: 题型:
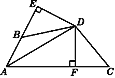
查看答案和解析>>【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF.
(1)求证:AD平分∠BAC;
(2)猜想写出AB+AC与AE之间的数量关系并给予证明.
-
科目: 来源: 题型:
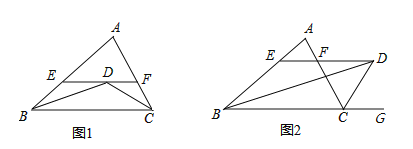
查看答案和解析>>【题目】(1)如图1所示,在△ABC中,EF∥BC,点D在EF上,BD、CD分别平分∠ABC、∠ACB,若已知BE=3,CF=5,求EF的长度;
(2)如图2所示,BD平分∠ABC、CD平分∠ACG,DE∥BC交AB于点E,交AC于点F,线段EF与BE、CF有什么数量关系?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD.
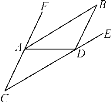
(1)判断∠FAB与∠C的大小关系,请说明理由;
(2)若∠C=35°,AB是∠FAD的平分线.
①求∠FAD的度数;
②若∠ADB=110°,求∠BDE的度数.
-
科目: 来源: 题型:
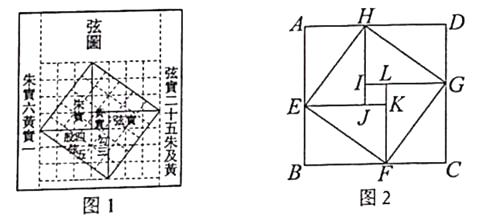
查看答案和解析>>【题目】我国三国时期数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”,如图1所示.在图2中,若正方形ABCD的边长为14,正方形IJKL的边长为2,且IJ//AB,则正方形EFGH的边长为.
相关试题

