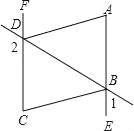
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

参考答案:
【答案】(1)平行,理由见解析(2) 平行,理由见解析(3) 平分,理由见解析
【解析】
(1)证明∠1=∠CDB,利用同位角相等,两直线平行即可证得;
(2)平行,根据平行线的性质可以证得∠A=∠CBE,然后利用平行线的判定方法即可证得;
(3)∠EBC=∠CBD,根据平行线的性质即可证得.
解:(1)平行.理由如下:
∵∠1+∠2=180°,∠2+∠CDB=180°(邻补角定义),
∴∠1=∠CDB,
∴AE∥FC( 同位角相等两直线平行);
(2)平行.理由如下:
∵AE∥CF,
∴∠C=∠CBE(两直线平行,内错角相等),
又∵∠A=∠C,
∴∠A=∠CBE,
∴AD∥BC(同位角相等,两直线平行);
(3)平分.理由如下:
∵DA平分∠BDF,
∴∠FDA=∠ADB,
∵AE∥CF,AD∥BC,
∴∠FDA=∠A=∠CBE,∠ADB=∠CBD,
∴∠EBC=∠CBD,
∴BC平分∠DBE.
-
科目: 来源: 题型:
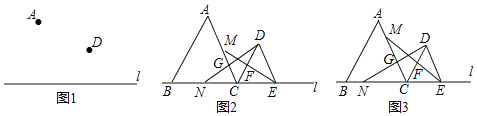
查看答案和解析>>【题目】已知点A、D在直线l的同侧.
(1)如图1,在直线l上找一点C.使得线段AC+DC最小(请通过画图指出点C的位置);
(2)如图2,在直线l上取两点B、E,恰好能使△ABC和△DCE均为等边三角形.M、N分别是线段AC、BC上的动点,连结DN交AC于点G,连结EM交CD于点F.
①当点M、N分别是AC、BC的中点时,判断线段EM与DN的数量关系,并说明理由;
②如图3,若点M、N分别从点A和B开始沿AC和BC以相同的速度向点C匀速运动,当M、N与点C重合时运动停止,判断在运动过程中线段GF与直线1的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC;
(2)若AB=4,AD=
 ,AE=3,求AF的长.
,AE=3,求AF的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次中学生田径运动会上,根据参加男子跳高初赛的运动员的成绩(单位:m),绘制出如下的统计图①和图②,请根据相关信息,解答下列问题:

(Ⅰ)图1中a的值为 ;
(Ⅱ)求统计的这组初赛成绩数据的平均数、众数和中位数;
(Ⅲ)根据这组初赛成绩,由高到低确定9人进入复赛,请直接写出初赛成绩为1.65m的运动员能否进入复赛.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4个完全相同的小球,分别标有数字1,2,3,4,另外有一个可以自由旋转的圆盘,被分成面积相等的3个扇形区域,分别标有数字1,2,3(如图所示).

(1)从口袋中摸出一个小球,所摸球上的数字大于2的概率为 ;
(2)小龙和小东想通过游戏来决定谁代表学校参加歌咏比赛,游戏规则为:一人从口袋中摸出一个小球,另一人转动圆盘,如果所摸球上的数字与圆盘上转出数字之和小于5,那么小龙去;否则小东去.你认为游戏公平吗?请用树状图或列表法说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
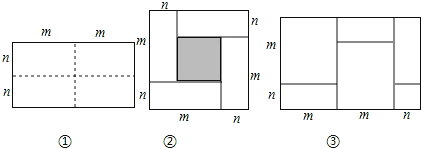
(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于 ;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:
方法2:
③观察图②,请写出代数式(m+n)2,(m﹣n)2,mn这三个代数式之间的等量关系: ;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n﹣6|+|mn﹣4|=0,求(m﹣n)2的值.
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料:
《张丘建算经》是一部数学问题集,其内容、范围与《九章算术》相仿.其中提出并解决了一个在数学史上非常著名的不定方程问题,通常称为“百鸡问题”:“今有鸡翁一值钱五,鸡母一值钱三,鸡雏三值钱一,凡百钱买鸡百只,问鸡翁、母、雏各几何.”
译文:公鸡每只值五文钱,母鸡每只值三文钱,小鸡每三只值一文钱,现在用一百文钱买一百只鸡,问这一百只鸡中,公鸡、母鸡、小鸡各有多少只?结合你学过的知识,解决下列问题:
(1)若设公鸡有x只,母鸡有y只,
①则小鸡有______只,买小鸡一共花费______文钱;(用含x,y的式子表示)
②根据题意列出一个含有x,y的方程:______;
(2)若对“百鸡问题”增加一个条件:公鸡数量是母鸡数量的3倍,求此时公鸡、母鸡、小鸡各有多少只?
相关试题

