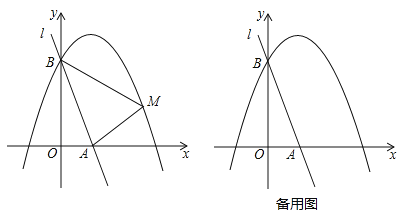
【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线![]() (a<0)经过点B.
(a<0)经过点B.
(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
参考答案:
【答案】(1)![]() ;(2)S=
;(2)S=![]() ,当m=
,当m=![]() 时,S取得最大值
时,S取得最大值![]() ;(3)①M′(
;(3)①M′(![]() ,
,![]() );②45°.
);②45°.
【解析】
试题分析:(1)利用直线l的解析式求出B点坐标,再把B点坐标代入二次函数解析式即可求出a的值;
(2)设M的坐标为(m,![]() ),然后根据面积关系将△ABM的面积进行转化;
),然后根据面积关系将△ABM的面积进行转化;
(3)①由(2)可知m=![]() ,代入二次函数解析式即可求出纵坐标的值;
,代入二次函数解析式即可求出纵坐标的值;
②可将求d1+d2最大值转化为求AC的最小值.
试题解析:(1)令x=0代入y=﹣3x+3,∴y=3,∴B(0,3),把B(0,3)代入![]() ,∴3=a+4,∴a=﹣1,∴二次函数解析式为:
,∴3=a+4,∴a=﹣1,∴二次函数解析式为:![]() ;
;
(2)令y=0代入![]() ,∴
,∴![]() ,∴x=﹣1或3,∴抛物线与x轴的交点横坐标为﹣1和3,∵M在抛物线上,且在第一象限内,∴0<m<3,令y=0代入y=﹣3x+3,∴x=1,∴A的坐标为(1,0),由题意知:M的坐标为(m,
,∴x=﹣1或3,∴抛物线与x轴的交点横坐标为﹣1和3,∵M在抛物线上,且在第一象限内,∴0<m<3,令y=0代入y=﹣3x+3,∴x=1,∴A的坐标为(1,0),由题意知:M的坐标为(m,![]() ),S=S四边形OAMB﹣S△AOB
),S=S四边形OAMB﹣S△AOB
=S△OBM+S△OAM﹣S△AOB=![]() ×m×3+
×m×3+![]() ×1×(
×1×(![]() )﹣
)﹣![]() ×1×3=
×1×3=![]() ,∵S=
,∵S=![]() =
=![]() ,∴当m=
,∴当m=![]() 时,S取得最大值
时,S取得最大值![]() .
.

(3)①由(2)可知:M′的坐标为(![]() ,
,![]() );
);
②过点M′作直线l1∥l′,过点B作BF⊥l1于点F,根据题意知:d1+d2=BF,此时只要求出BF的最大值即可,∵∠BFM′=90°,∴点F在以BM′为直径的圆上,设直线AM′与该圆相交于点H,∵点C在线段BM′上,∴F在优弧![]() 上,∴当F与M′重合时,BF可取得最大值,此时BM′⊥l1,∵A(1,0),B(0,3),M′(
上,∴当F与M′重合时,BF可取得最大值,此时BM′⊥l1,∵A(1,0),B(0,3),M′(![]() ,
,![]() ),∴由勾股定理可求得:AB=
),∴由勾股定理可求得:AB=![]() ,M′B=
,M′B=![]() ,M′A=
,M′A=![]() ,过点M′作M′G⊥AB于点G,设BG=x,∴由勾股定理可得:
,过点M′作M′G⊥AB于点G,设BG=x,∴由勾股定理可得:![]() ,∴
,∴![]() ,∴x=
,∴x=![]() ,cos∠M′BG=
,cos∠M′BG=![]() =
=![]() ,∵l1∥l′,∴∠BCA=90°,∠BAC=45°;
,∵l1∥l′,∴∠BCA=90°,∠BAC=45°;

方法二:过B点作BD垂直于l′于D点,过M点作ME垂直于l′于E点,则BD=d1,ME=d2,∵S△ABM=![]() ×AC×(d1+d2),当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM时取得最小值.
×AC×(d1+d2),当d1+d2取得最大值时,AC应该取得最小值,当AC⊥BM时取得最小值.
根据B(0,3)和M′(![]() ,
,![]() )可得BM′=
)可得BM′=![]() ,∵S△ABM=
,∵S△ABM=![]() ×AC×BM′=
×AC×BM′=![]() ,∴AC=
,∴AC=![]() ,当AC⊥BM′时,cos∠BAC=
,当AC⊥BM′时,cos∠BAC=![]() =
=![]() =
=![]() ,∴∠BAC=45°.
,∴∠BAC=45°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】_____一件事情的语句叫做命题,命题常可以写成“如果……那么……”的形式,“如果”后面接的部分是____________,“那么”后面接的部分是___________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形与所描述的一致的是( )
A.等边三角形是中心对称图形
B.所有直角三角形都是轴对称图形
C.所有平行四边形都是中心对称图形
D.正五边形是中心对称图形
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的个数有( )
①射线AB与射线BA表示同一条射线.
②若∠1+∠2=180°,∠1+∠3=180°,则∠2=∠3.
③一条射线把一个角分成两个角,这条射线叫这个角的平分线.
④连结两点的线段叫做两点之间的距离.
⑤40°50ˊ=40.5°.
⑥互余且相等的两个角都是45°.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:已知在纸面上有一数轴(如图所示),

操作一:
(1)折叠纸面,使表示的1点与﹣1表示的点重合,则﹣3表示的点与表示的点重合;
操作二:
(2)折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数表示的点重合; -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
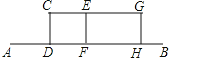
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t 取任何符合条件的实数,点A,P 都在抛物线C 上.
(1)当t=-5时,求抛物线C 的对称轴;
(2)当-60≤n≤-30 时,判断点(1,n)是否在抛物线C上, 并说明理由;
(3)如图,若点A在x轴上,过点A作线段AP的垂线交y轴于点B,交抛物线C于点D,当点D的纵坐标为m+
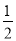 时,求S△PAD的最小值.
时,求S△PAD的最小值. 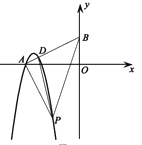
相关试题

