【题目】已知抛物线C:y=(x+2)[t(x+1)-(x+3)],其中-7≤t≤-2,且无论t 取任何符合条件的实数,点A,P 都在抛物线C 上.
(1)当t=-5时,求抛物线C 的对称轴;
(2)当-60≤n≤-30 时,判断点(1,n)是否在抛物线C上, 并说明理由;
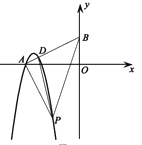
(3)如图,若点A在x轴上,过点A作线段AP的垂线交y轴于点B,交抛物线C于点D,当点D的纵坐标为m+![]() 时,求S△PAD的最小值.
时,求S△PAD的最小值.
参考答案:
【答案】(1)当t=-5时,求抛物线C 的对称轴为x=-![]()
(2)当-60≤n<-54时,点(1,n)不在抛物线C上,当-54≤n≤-30时,点(1,n)在抛物线C上,理由见解析;
(3)S△PAD的最小值为![]()
【解析】试题分析:(1)把t=5代入y=(x+2)[t(x+1)-(x+3)],求出函数解析式,在根据对称轴x=-![]() 计算得出;(2) 假设(1,n)在抛物线上,将点(1,n)代入解析式,得n=6t-12,在根据-7≤t≤-2, 得出当-60≤n<-54时,点(1,n)不在抛物线C上; 当-54≤n≤-30时,点(1,n)在抛物线C上;(3) 根据点A是抛物线与x轴的交点, 点P在抛物线C 上, 求出A(-2,0),P(-1,-2), 过点P作PN⊥x轴于点N,证△PAN≌△ABO, 得到BO=1, PA=AB=
计算得出;(2) 假设(1,n)在抛物线上,将点(1,n)代入解析式,得n=6t-12,在根据-7≤t≤-2, 得出当-60≤n<-54时,点(1,n)不在抛物线C上; 当-54≤n≤-30时,点(1,n)在抛物线C上;(3) 根据点A是抛物线与x轴的交点, 点P在抛物线C 上, 求出A(-2,0),P(-1,-2), 过点P作PN⊥x轴于点N,证△PAN≌△ABO, 得到BO=1, PA=AB=![]() ,过点D作DM⊥x轴于点M,证△DAM∽△BAO,得S△PAD=
,过点D作DM⊥x轴于点M,证△DAM∽△BAO,得S△PAD=![]() ,当m取最小值-
,当m取最小值-![]() 时, S△PAD的最小值为
时, S△PAD的最小值为![]() .
.
试题解析:
(1)当t=5时,y=-6x2-20x-16,
∵-![]() =-
=-![]() ,
,
∴对称轴为x=-![]() .
.
(2)若(1,n)在抛物线上,
将点(1,n)代入解析式,得
n=6t-12.
∵ -7≤t≤-2,
∴ -54≤n≤-24.
∵ -60≤n≤-30,
∴ 当-60≤n<-54时,点(1,n)不在抛物线C上;
当-54≤n≤-30时,点(1,n)在抛物线C上.
(3)由题得A(-2,0),P(-1,-2).
过点P作PN⊥x轴于点N,可得
PN=AO=2,∠PNA=∠AOB=90°.
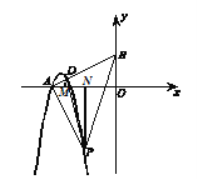
∵ PA⊥AB,
∴ ∠PAN+∠BAO=90°.
又∵ ∠ABO+∠BAO=90°,
∴ ∠PAN=∠ABO.
∴ △PAN≌△ABO.
∴ BO=1,
PA=AB=![]() .
.
过点D作DM⊥x轴于点M,可得
∠DMA=∠BOA=90°.
又∵ ∠DAM=∠BAO,
∴ △DAM∽△BAO.
∴ ![]() .
.
∴ AD=![]() .
.
∴ S△PAD=![]() APAD=
APAD=![]() .
.
∵ A(-2,0),B(0,1),
∴ 直线AB的解析式为y=![]() x+1.
x+1.
当y=m+![]() 时,x=2m-1.
时,x=2m-1.
把点D(2m-1,m+![]() )代入抛物线C的解析式,得t=1+
)代入抛物线C的解析式,得t=1+![]() .
.
∵ -7≤t≤-2,
∴ -![]() ≤m≤-
≤m≤-![]() .
.
∴ m+![]() >0.
>0.
∴ S△PAD=![]() (m+
(m+![]() ).
).
∵ ![]() >0,
>0,
∴ S△PAD随m的增大而增大.
∴ 当m取最小值-![]() 时, S△PAD的最小值为
时, S△PAD的最小值为![]() .
.
点睛:以二次函数为背景的几何图形变换问题,其核心思想方法主要有分类讨论思想,函数与方程思想,树形结合思想,转化思想,待定系数法,配方法等,要用运动和变化的眼光去观察,研究图形,抓住其中的等量关系和变量关系,综合分析问题 和解决问题的能力.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线l:y=﹣3x+3与x轴、y轴分别相交于A、B两点,抛物线
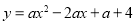 (a<0)经过点B.
(a<0)经过点B.(1)求该抛物线的函数表达式;
(2)已知点M是抛物线上的一个动点,并且点M在第一象限内,连接AM、BM,设点M的横坐标为m,△ABM的面积为S,求S与m的函数表达式,并求出S的最大值;
(3)在(2)的条件下,当S取得最大值时,动点M相应的位置记为点M′.
①写出点M′的坐标;
②将直线l绕点A按顺时针方向旋转得到直线l′,当直线l′与直线AM′重合时停止旋转,在旋转过程中,直线l′与线段BM′交于点C,设点B、M′到直线l′的距离分别为d1、d2,当d1+d2最大时,求直线l′旋转的角度(即∠BAC的度数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作探究:已知在纸面上有一数轴(如图所示),

操作一:
(1)折叠纸面,使表示的1点与﹣1表示的点重合,则﹣3表示的点与表示的点重合;
操作二:
(2)折叠纸面,使﹣1表示的点与3表示的点重合,回答以下问题:
①5表示的点与数表示的点重合; -
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法);
(2)求小明原来的速度.
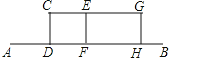
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将第一个图(图①)所示的正三角形连结各边中点进行分割,得到第二个图(图②);再将第二个图中最中间的小正三角形按同样的方式进行分割,得到第三个图(图③);再将第三个图中最中间的小正三角形按同样的方式进行分割,…,则得到的第五个图中,共有个正三角形.( )
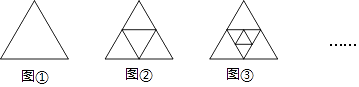
A.14
B.15
C.16
D.17 -
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形具有而菱形不具有的性质是( )
A. 对角线互相平分 B. 对角线相等
C. 对角线平分一组对角 D. 对角线互相垂直
相关试题

