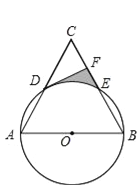
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F.
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
参考答案:
【答案】(1)证明见试题解析;(2)![]() (3)
(3)![]() ﹣
﹣![]() π.
π.
【解析】
试题分析:(1)连接OD,如图,利用等边三角形的性质得到∠A=∠C=60°,再证明OD∥BC,然后利用DF⊥BC可得OD⊥BC,再根据切线的判定定理可判断DF为⊙O的切线;
(2)利用等边三角形的性质得到AB=AC=4,∠C=60°,则CD=2,然后在Rt△CDF中利用正弦的定义可计算出DF;
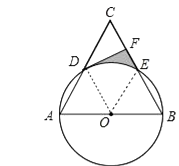
(3)连接OE,如图,根据扇形的面积公式,利用S阴影部分=S梯形ODFE﹣S扇形DOE进行计算.
试题解析:(1)连接OD,如图,∵△ABC为等边三角形,∴∠A=∠C=60°,
∵OA=OD,∴∠ODA=∠A=60°,∴∠ODA=∠C,∴OD∥BC,∵DF⊥BC,
∴OD⊥BC,∴DF为⊙O的切线;
(2)∵等边三角形ABC的边长为4,∴AB=AC=4,∠C=60°,∵AO=AD=2,
∴CD=2,在Rt△CDF中,∵sinC=![]() ,∴DF=2sin60°=
,∴DF=2sin60°=![]() ;
;
(3)连接OE,如图,∵CF=![]() CD=1,∴EF=CE﹣CF=1,
CD=1,∴EF=CE﹣CF=1,
∴S阴影部分=S梯形ODFE﹣S扇形DOE=![]() (1+2)
(1+2)![]() ﹣
﹣![]() =
=![]() ﹣
﹣![]() π.
π.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据2,﹣4,x,6,﹣8的众数为6,则这组数据的中位数为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将二次函数y=x2的图象向下平移2个单位,再向右平移3个单位,则平移后的二次函数的解析式为( )
A.y=x2﹣2
B.y=x2+2
C.y=(x+3)2+2
D.y=(x﹣3)2﹣2 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知,EG∥AF,请你从下面三个条件中,再选出两个作为已知条件,另一个作为结论,推出一个正确的命题。并证明这个命题(只写出一种情况)①AB=AC; ②DE=DF; ③BE=CF。(在已知和求证中,填写正确序号)
已知:EG∥AF,_______,_________.
求证:__________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A. 3x+2x2=5x2 B. ﹣ab﹣ab=﹣2ab C. 2a2b-a2b=1 D. 7x+5x=12x2
-
科目: 来源: 题型:
查看答案和解析>>【题目】不等式3x﹣2≤5x+6的所有负整数解的和为
-
科目: 来源: 题型:
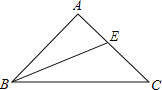
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,BE平分∠ABC交AC于E,若∠A=90°,那么BC、BA、AE三者之间有何关系?并加以证明.
相关试题

