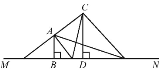
【题目】如图,AB⊥MN,CD⊥MN,垂足分别为B,D,AB=2,CD=4,BD=3.若在直线MN上存在点P,能使△PAB与△PCD相似,则PB=_____
参考答案:
【答案】3或1或![]()
【解析】
分三种情形①延长CA交MN于P1,此时△P1AB∽△P1CD.②当点P2在BD上时.③当点P3在BD的延长线时.分别列出方程即可即可.
如图,
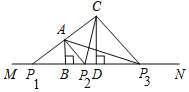
①延长CA交MN于P1,
∵AB⊥MN,CD⊥MN,
∴AB∥CD
∴△P1AB∽△P1CD,
∴![]() ,
,
∴P1B=BD=3.
②当点P2在BD上时,设P2B=x,若△ABP2∽△CDP2则有![]() ,
,
∴![]() ,
,
∴x=1,
∴P2B=1,
若△ABP2∽△P2DC,则有![]() ,方程无解.
,方程无解.
③当点P3在BD的延长线时,∵△P3AB∽△CP3D,
∴![]() ,
,
∴![]() ,
,
∴x=![]() 或
或![]() (舍弃)
(舍弃)
∴P3B=![]() ,
,
综上所述,满足条件的PB的长为3或1或![]() .
.
-
科目: 来源: 题型:
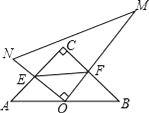
查看答案和解析>>【题目】在Rt△ACB中,∠C=90°,AC=BC,一直角三角板的直角顶角O在AB边的中点上,这块三角板绕O点旋转,两条直角边始终与AC、BC边分别相交于E、F,连接EF,则在运动过程中,△OEF与△ABC的关系是( )
A. 一定相似 B. 当E是AC中点时相似
C. 不一定相似 D. 无法判断
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=
 AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则
AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则 的值为( )
的值为( )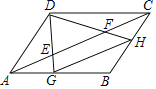
A.
 B.
B.  C.
C.  D. 1
D. 1 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
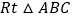 中,
中,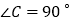 ,
,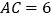 ,
,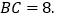 在
在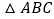 内并排
内并排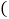 不重叠
不重叠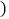 放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放
放入边长为1的小正方形纸片,第一层小纸片的一条边都在AB上,首尾两个正方形各有一个顶点分别在AC、BC上,依次这样摆放上去,则最多能摆放
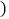 个小正方形纸片.
个小正方形纸片.
A. 14个 B. 15个 C. 16个 D. 17个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形
 为长方形,点
为长方形,点 在
在 轴上,点
轴上,点 在
在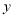 轴上,
轴上,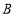 点坐标为
点坐标为 ,将
,将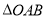 沿
沿 翻折,
翻折, 的对应点为
的对应点为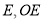 交
交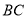 于点
于点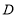 ,则
,则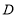 点的坐标为__________.
点的坐标为__________.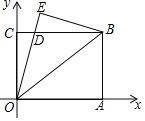
-
科目: 来源: 题型:
查看答案和解析>>【题目】小颖根据学习函数的经验,对函数
 的图象与性质进行了探究,下面是小颖的探究过程,请你补充完整.
的图象与性质进行了探究,下面是小颖的探究过程,请你补充完整.(1)列表:
x
…
-2
-1
0
1
2
3
4
…
y
…
-2
-1
0
1
0
-1
k
…
①
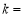 ____;
____;②若
 ,
, ,
,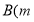 ,
, 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则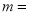 ____;
____;(2)描点并画出该函数的图象;
(3)①根据函数图象可得:该函数的最大值为____;
②观察函数
 的图象,写出该图象的两条性质________________________;_____________________;
的图象,写出该图象的两条性质________________________;_____________________;③已知直线
 与函数
与函数 的图象相交,则当
的图象相交,则当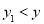 时,
时,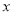 的取值范围为是____.
的取值范围为是____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条笔直的公路上有A、B两地,甲骑自行车从A地到B地;乙骑自行车从B地到A地,到达A地后立即按原路返回,如图是甲、乙两人离B地的距离y(km)与行驶时x(h)之间的函数图象,根据图象解答以下问题:
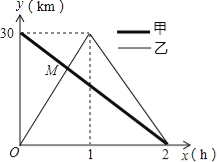
(1)写出A、B两地直接的距离;
(2)求出点M的坐标,并解释该点坐标所表示的实际意义;
(3)若两人之间保持的距离不超过3km时,能够用无线对讲机保持联系,请直接写出甲、乙两人能够用无线对讲机保持联系时x的取值范围.
相关试题

