【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.

(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
参考答案:
【答案】(1)证明见解析;(2)90°.
【解析】
试题分析:(1)根据旋转的性质得CE=CD,∠DCE=90°,则利用等角的余角相等可得∠ECF=∠BCD,于是可根据“SAS”判断△BCD≌△FCE;
(2)根据2平行线的性质得∠CEF+∠DCE=180°,加上∠DCE=90°,所以∠CEF=90°,于是得到∠BDC=90°.
试题解析:(1)∵线段CD绕点C按顺时针方向旋转90°后得CE,
∴CE=CD,∠DCE=90°,
∵∠ACB=90°,
∴∠ECF=∠BCD,
在△BCD和△FCE中

∴△BCD≌△FCE,
(2)∵EF∥CD,
∴∠CEF+∠DCE=180°,
而∠DCE=90°,
∴∠CEF=90°,
∴∠BDC=90°.
-
科目: 来源: 题型:
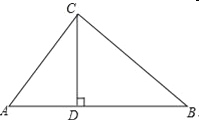
查看答案和解析>>【题目】如图,在公路AB旁有一座山,现C处需要爆破.已知点C与公路上的停靠站A的距离为300m,与公路上另一停靠站B的距离为400m,且CA⊥CB,CD⊥AB,为了安全起见,爆破点C周围半径250m范围内不得进入,问在进行爆破时,公路AB段是否因有危险而需要暂时封锁?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,连接CD.

(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM与⊙O相切?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:
A.非常了解 B.比较了解 C.基本了解 D.不了解
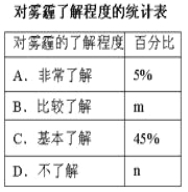
根据调查统计结果,绘制了下面的三种统计图表.

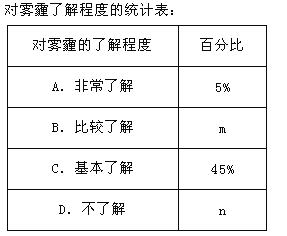
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有多少人?求出表中m和n的值.
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角的度数.
(3)请补全图1所示的条形统计图.
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义新运算:a⊕b=ab﹣a,例如:3⊕2=3×2﹣3=3,则(﹣3)⊕4=( )
A. ﹣9 B. 12 C. ﹣15 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=3x-1的图像在y轴上的截距是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面事件:①掷一枚硬币,着地时正面向上;②在标准大气压下,水加热到100℃会沸腾;③买一张福利彩票,开奖后会中奖;④明天会下雨.其中,必然事件有( )
A. 1个 B. 2个 C. 3个 D. 4个
相关试题

