Question

【题目】在正方形ABCD中，过点A引射线AH，交边CD于点H（点H与点D不重合）．通过翻折，使点B落在射线AH上的点G处，折痕AE交BC于E，延长EG交CD于F．
（1）如图①，当点H与点C重合时，可得FGFD．（大小关系）

（2）如图②，当点H为边CD上任意一点时，猜想FG与FD的数量关系，并说明理由．

（3）在图②中，当AB=8，BE=3时，利用探究的结论，求CF的长．

Answer 1

【答案】
（1）=
（2）

解：猜想FD=FG．

证明：连接AF，

由折叠的性质可得AB=AG=AD，

在Rt△AGF和Rt△ADF中，

，

∴△AGF≌△ADF．

∴FG=FD

（3）

解：设FG=x，

∵AB=8，BE=3，

∴BC=CD=8，

∴FC=8﹣x，FE=3+x，EC=8﹣3=5，

在Rt△ECF中，EF2=FC2+EC2，即（3+x）2=（8﹣x）2+52，

解得x= ．

∴CF=8﹣ = ，

即FG的长为

【解析】解：（1）连接AF，
由折叠的性质可得AB=AG=AD，
在Rt△AGF和Rt△ADF中，
，
∴△AGF≌△ADF．
∴FG=FD．
故答案为：=；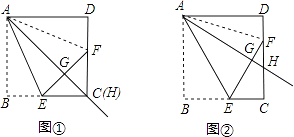

（1）连接AF，根据图形猜想FD=FG，由折叠的性质可得AB=AG=AD，再结合AF为△AGF和△ADF的公共边，从而证明△AGF≌△ADF，从而得出结论．（2）连接AF，根据图形猜想FD=FG，由折叠的性质可得AB=AG=AD，再结合AF为△AGF和△ADF的公共边，从而证明△AGF≌△ADF，从而得出结论．（3）设FG=x，则FC=8﹣x，FE=3+x，在Rt△ECF中利用勾股定理可求出x的值，进而可得出答案．