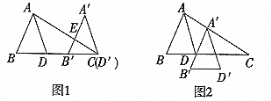
【题目】如图1,平移三角形ABD,使点D沿BD的延长线平移至点C,得到三角形![]() ,
,![]() 交AC于点E,AD平分∠BAC.
交AC于点E,AD平分∠BAC.
(1)猜想![]() 与
与![]() 之间的关系,并写出理由;
之间的关系,并写出理由;
(2)如果将三角形ABD平移至如图2所示位置,得到三角形![]() ,请问
,请问![]() 平分
平分![]() 吗?为什么?
吗?为什么?
参考答案:
【答案】(1)∠B′EC=2∠A′,理由见解析;(2)A′D′平分∠B′A′C,理由见解析.
【解析】
(1)根据平移的性质得出∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,进而得出∠BAC=∠B′EC,进而得出答案;
(2)利用平移的性质得出∠B′A′D′=∠BAD,AB∥A′B′,进而得出∠BAD=![]() ∠BAC,即可得出∠B′A′D′=
∠BAC,即可得出∠B′A′D′=![]() ∠B′A′C.
∠B′A′C.
(1)∠B′EC=2∠A′,
理由:∵将△ABD平移,使D沿BD延长线移至C得到△A′B′D′,A′B′交AC于E,AD平分∠BAC,
∴∠BAD=∠DAC,∠BAD=∠A′,AB∥A′B′,
∴∠BAC=∠B′EC,
∴∠BAD=∠A′=![]() ∠BAC=
∠BAC=![]() ∠B′EC,
∠B′EC,
即∠B′EC=2∠A′;
(2)A′D′平分∠B′A′C,
理由:∵将△ABD平移至如图(2)所示,得到△A′B′D′,
∴∠B′A′D′=∠BAD,AB∥A′B′,
∴∠BAC=∠B′A′C,
∵∠BAD=![]() ∠BAC,
∠BAC,
∴∠B′A′D′=![]() ∠B′A′C,
∠B′A′C,
∴A′D′平分∠B′A′C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点M是Rt△ABC的斜边AB的中点,连接CM,作线段CM的垂直平分线,分别交边CB和CA的延长线于点D、E,若∠C=90°,AB=20,tanB=
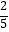 ,则DE= .
,则DE= . 
-
科目: 来源: 题型:
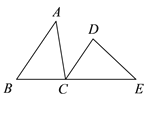
查看答案和解析>>【题目】如图,B、C、E 三点在同一条直线上,AB∥DC,BC=DC,∠ACD=∠E.
求证:(1)∠ACB=∠D;
(2)AB=EC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在以AB为直径的半圆上,AB=4
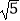 ,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是 .
,AC=4,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE,DF交EC的延长线于点F,当点D从点A运动到点B时,线段EF扫过的面积是 . 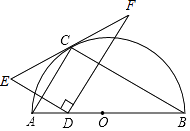
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是_____(用字母n表示).
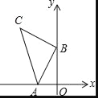
-
科目: 来源: 题型:
查看答案和解析>>【题目】体育中考前,抽样调查了九年级学生的“1分钟跳绳”成绩,并绘制成了下面的频数分布直方图(每小组含最小值,不含最大值)和扇形图.

(1)补全频数分布直方图;
(2)扇形图中m=;
(3)若“1分钟跳绳”成绩大于或等于140次为优秀,则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人?
相关试题

