Question

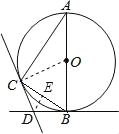
【题目】如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC=120°，连接AC．

（1）求∠A的度数；

（2）若点D到BC的距离为2，那么⊙O的半径是多少？

Answer 1

【答案】(1)30°；(2)4

【解析】

试题分析：(1)首先连接OC，由BD，CD分别是过⊙O上点B，C的切线，可求得∠BOC的度数，然后由圆周角定理，求得答案；(2)首先求得∠DCB与∠DBC的度数，然后过点D作DE⊥BC，垂足为E，则DE=2，即可求得BE的长，继而求得BC的长，然后由(1)可知△OBC为等边三角形，即可求得答案．

试题解析：(1)连接OC， ∵BD，CD分别是过⊙O上点B，C的切线， ∴OC⊥CD，OB⊥BD，

∴∠OCD=∠OBD=90°， ∵∠BDC=120°， ∴∠BOC=360°﹣∠OCD﹣∠BDC﹣∠OBD=60°，

∴∠A=∠BOC=30°；

(2)∵BD，CD分别是过⊙O上点B，C的切线， ∴DC=DB，

∴∠DCB=∠DBC=（180°﹣120°）=30°， 过点D作DE⊥BC，垂足为E，则DE=2， ∵∠DBC=30°，

∴BD=2DE=4， 在直角△DEB中，BE=2， ∴BC=2BE=4，

由(1)可知△OBC为等边三角形， ∴OB=BC=4， ∴⊙O的半径是4.