[题目]有一个几何体的形状为直三棱柱.右图是它的主视图和左视图．(1)请补画出它的俯视图.并标出相关数据,(2)根据图中所标的尺寸(单位:厘米).计算这个几何体的全面积．题目和参考答案 ——青夏教育精英家教网—

【题目】有一个几何体的形状为直三棱柱，右图是它的主视图和左视图．

(1)请补画出它的俯视图，并标出相关数据；

(2)根据图中所标的尺寸(单位：厘米)，计算这个几何体的全面积．

参考答案：

【答案】（1）见解析（2）120平方厘米

【解析】分析：（1）观察图形可知，俯视图是一个长8宽3的长方形，据此画出图形即可；

（2）先根据勾股定理得到斜边长为10厘米，再根据表面积=3个长方形的面积+2个三角形的面积，列出算式计算即可求解．

本题解析：

解：(1)如图所示；

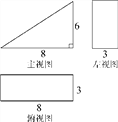
(2)由勾股定理得斜边长为10厘米，S底＝×8×6＝24(平方厘米)，S侧＝(8＋6＋10)×3＝72(平方厘米)，S全＝72＋24×2＝120(平方厘米)．

答：这个几何体的全面积是120平方厘米．

相关试题

科目： 来源： 题型：

【题目】如图，Rt△ABO的顶点A是双曲线y＝与直线y＝－x－(k＋1)在第二象限的交点．AB⊥x轴于B，且S△ABO＝．
(1)求这两个函数的解析式；
(2)求直线与双曲线的两个交点A．C的坐标和△AOC的面积．
查看答案和解析>>
科目： 来源： 题型：

【题目】一学员在广场上练习驾驶汽车，两次拐弯后，行驶方向与原来的方向相同，这两次拐弯的角度可能是（）
A．第一次向左拐50°，第二次向左拐50° B．第一次向左拐50°，第二次向右拐50°
C．第一次向右拐50°，第二次向右拐130° D．第一次向左拐50°，第二次向左拐130°
查看答案和解析>>
科目： 来源： 题型：

【题目】通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．

原题：如图1，点E、F分别在正方形ABCD的边BC、CD上，∠EAF＝45°，连接EF，则EF＝BE＋DF，试说明理由．
（1）思路梳理
∵AB＝CD，
∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．
∵∠ADC＝∠B＝90°，
∴∠FDG＝180°，点F、D、G共线．
根据___________，SAS
易证△AFG≌___________△AEF
，得EF＝BE＋DF．
（2）类比引申
如图2，四边形ABCD中，AB＝AD，∠BAD＝90°．点E、F分别在边BC、CD上，∠EAF＝45°．若∠B、∠D都不是直角，则当∠B与∠D满足等量关系______________∠B+∠D=180°
时，仍有EF＝BE＋DF．
（3）联想拓展
如图3，在△ABC中，∠BAC＝90°，AB＝AC，点D、E均在边BC上，且∠DAE＝45°．猜想BD、DE、EC应满足的等量关系，并写出推理过程．
查看答案和解析>>
科目： 来源： 题型：

【题目】如图，在△ABC中，BE，CD分别为其角平分线且交于点O.
(1)当∠A＝60°时，求∠BOC的度数；
(2)当∠A＝100°时，求∠BOC的度数；
(3)当∠A＝α时，求∠BOC的度数．
查看答案和解析>>
科目： 来源： 题型：

【题目】填写下面证明过程中的推理依据：
已知AD⊥BC，FG⊥BC，垂足分别为D、G，且∠1=∠2，求证∠BDE=∠C．
证明：∵AD⊥BC，FG⊥BC （已知），
∴∠ADC=∠FGC=90°____________．
∴AD∥FG______________________．
∴∠1=∠3___________________
又∵∠1=∠2，（已知），
∴∠3=∠2____________．
∴ED∥AC_____________．
∴∠BDE=∠C______________．
查看答案和解析>>
科目： 来源： 题型：

【题目】(1)如图，在△ABC中，D，E，F是边BC上的三点，且∠1＝∠2＝∠3＝∠4，以AE为角平分线的三角形有_________；
(2)如图，已知AE平分∠BAC，且∠1＝∠2＝∠4＝15°，计算∠3的度数，并说明AE是△DAF的角平分线．
查看答案和解析>>