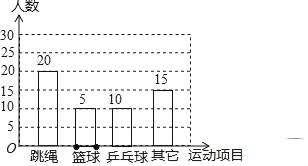
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
参考答案:
【答案】(1)5,20,80;(2)图见解析;(3)![]() .
.
【解析】试题分析:(1)先利用跳绳的人数和它所占的百分比计算出调查的总人数,再用总人数分别减去喜欢其它项目的人数可得到喜欢篮球项目的人数,再计算出喜欢乒乓球项目的百分比,然后用800乘以样本中喜欢篮球项目的百分比可估计全校学生中喜欢篮球项目的人数;
(2)根据(1)中求得的数据可补充完整统计图;
(3)画树状图展示所有20种等可能的结果数,再找出所抽取的2名同学恰好是1名女同学和1名男同学的结果数,然后根据概率公式求解.
试题解析:(1)调查的总人数为20÷40%=50(人),
所以喜欢篮球项目的同学的人数=50﹣20﹣10﹣15=5(人);
“乒乓球”的百分比=![]() =20%,
=20%,
因为800×![]() =80,
=80,
所以估计全校学生中有80人喜欢篮球项目;
故答案为5,20,80;
(2)如图,
(3)画树状图为:

共有20种等可能的结果数,其中所抽取的2名同学恰好是1名女同学和1名男同学的结果数为12,
所以所抽取的2名同学恰好是1名女同学和1名男同学的概率=![]() =
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果关于x的一元二次方程ax2+bx+c=0有两个实数根,且其中一个根为另一个根的3倍,则称这样的方程为“立根方程”.以下关于立根方程的说法:
①方程x2﹣4x﹣12=0是立根方程;
②若点(p,q)在反比例函数y=
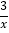 的图象上,则关于x的方程px2+4x+q=0是立根方程;
的图象上,则关于x的方程px2+4x+q=0是立根方程;③若一元二次方程ax2+bx+c=0是立根方程,且相异两点M(1+t,s),N(4﹣t,s)都在抛物线y=ax2+bx+c上,则方程ax2+bx+c=0的其中一个根是
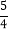 .
.正确的是( )
A. ①② B. ② C. ③ D. ②③
-
科目: 来源: 题型:
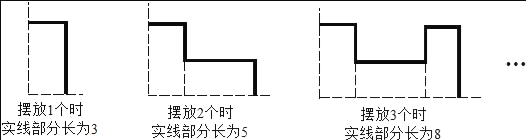
查看答案和解析>>【题目】将相同的矩形卡片,按如图方式摆放在一个直角上,每个矩形卡片长为2,宽为1,依此类推,摆放2014个时,实线部分长为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】顺次连接四边形ABCD四边中点得到新的四边形为菱形,那么原四边形ABCD为( )
A. 矩形
B. 菱形
C. 对角线相等的四边形
D. 对角线垂直的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某校一幢教学大楼的顶部竖有一块“传承文明,启智求真”的宣传牌CD.小明在山坡的坡脚A处测得宣传牌底部D的仰角为60°,沿山坡向上走到B处测得宣传牌顶部C的仰角为45°.已知山坡AB的坡度i=1:
 ,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据:
,AB=10米,AE=15米,求这块宣传牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: ≈1.414,
≈1.414, ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图表示购买某种商品的个数与付款数之间的关系
(1)根据图形完成下列表格
购买商品个数(个)
2
4
6
7
付款数(元)
(2)请写出表示付款数y(元)与购买这种商品的个数x(个)之间的关系式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形纸片ABCD折叠,使点D与点B重合,点C落在C′处,折痕为EF,若AB=1,BC=2,则△ABE和△BC′F的周长之和为( )

A. 3 B. 4 C. 6 D. 8
相关试题

