【题目】如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.动点M,N从点C同时出发,均以每秒1cm的速度分别沿CA、CB向终点A,B移动,同时动点P从点B出发,以每秒2cm的速度沿BA向终点A移动,连接PM,PN,设移动时间为t(单位:秒,0<t<2.5).
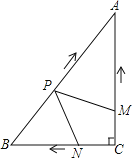
(1)当t为何值时,以A,P,M为顶点的三角形与△ABC相似?
(2)是否存在某一时刻t,使四边形APNC的面积S有最小值?若存在,求S的最小值;若不存在,请说明理由.
参考答案:
【答案】(1)当t=![]() 时,以A、P、M为顶点的三角形与△ABC相似;(2)当t=
时,以A、P、M为顶点的三角形与△ABC相似;(2)当t=![]() 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是![]() .
.
【解析】
试题分析:根据勾股定理求得AB=5cm.
(1)分类讨论:△AMP∽△ABC和△APM∽△ABC两种情况.利用相似三角形的对应边成比例来求t的值;
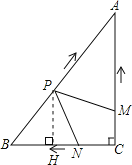
(2)如图,过点P作PH⊥BC于点H,构造平行线PH∥AC,由平行线分线段成比例求得以t表示的PH的值;然后根据“S=S△ABC﹣S△BPH”列出S与t的关系式S=![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
(0<t<2.5),则由二次函数最值的求法即可得到S的最小值.
解:∵如图,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根据勾股定理,得![]() =5cm.
=5cm.
(1)以A,P,M为顶点的三角形与△ABC相似,分两种情况:
①当△AMP∽△ABC时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=![]() ;
;
②当△APM∽△ABC时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得t=0(不合题意,舍去);
综上所述,当t=![]() 时,以A、P、M为顶点的三角形与△ABC相似;
时,以A、P、M为顶点的三角形与△ABC相似;
(2)存在某一时刻t,使四边形APNC的面积S有最小值.理由如下:
假设存在某一时刻t,使四边形APNC的面积S有最小值.
如图,过点P作PH⊥BC于点H.则PH∥AC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴PH=![]() t,
t,
∴S=S△ABC﹣S△BPN,
=![]() ×3×4﹣
×3×4﹣![]() ×(3﹣t)
×(3﹣t)![]() t,
t,
=![]() (t﹣
(t﹣![]() )2+
)2+![]() (0<t<2.5).
(0<t<2.5).
∵![]() >0,
>0,
∴S有最小值.
当t=![]() 时,S最小值=
时,S最小值=![]() .
.
答:当t=![]() 时,四边形APNC的面积S有最小值,其最小值是
时,四边形APNC的面积S有最小值,其最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 1的相反数是﹣1 B. 1的倒数是﹣1
C. 1的立方根是±1 D. ﹣1是无理数
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程9x2﹣6x+k=0有两个不相等的实根,则k的范围是( )
A.k<1
B.k>1
C.k≤1
D.k≥1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:x2+16x﹣k是完全平方式,则k=______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2017次运动后,动点P的坐标是______.

-
科目: 来源: 题型:
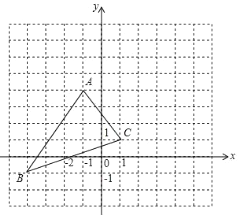
查看答案和解析>>【题目】如图,将三角形ABC向右平移5个单位长度,再向上平移3个单位长度请回答下列问题:
(1)平移后的三个顶点坐标分别为:A1( ),B1( ),C1( );
(2)画出平移后三角形A1B1C1;
(3)求三角形ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各多项式中,是二次三项式的是( )
A. a2+b2 B. x+y+7 C. 5-x-y2 D. x2-y2+x-3x2
相关试题

