【题目】如图是二次函数y=ax2+bx+c图象的一部分,过点(x1 , 0),﹣3<x1<﹣2,对称轴为直线x=﹣1.给出四个结论:①abc>0;②2a+b=0;③b2>4ac;④3b+2c>0,其中正确的结论有( ) 
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:①由抛物线的开口向下知a<0,与y轴的交点为在y轴的正半轴上, ∴c>0,对称轴为x=﹣ ![]() =﹣1,得2a=b,
=﹣1,得2a=b,
∴a、b同号,即b<0,
∴abc>0;
故本选项正确;②∵对称轴为x=﹣ ![]() =﹣1,得2a=b,
=﹣1,得2a=b,
∴2a﹣b=0;
故本选项错误;③从图象知,该函数与x轴有两个不同的交点,所以根的判别式△=b2﹣4ac>0,即b2>4ac;
故本选项正确;④∵﹣3<x1<﹣2,
∴根据二次函数图象的对称性,知当x=1时,y<0;
又由①知,2a=b,
∴a+b+c<0;
∴ ![]() b+b+c<0,
b+b+c<0,
即3b+2c<0;
故本选项错误.
综上所述,①③共有2个正确的.
故选B.
【考点精析】本题主要考查了二次函数图象以及系数a、b、c的关系的相关知识点,需要掌握二次函数y=ax2+bx+c中,a、b、c的含义:a表示开口方向:a>0时,抛物线开口向上; a<0时,抛物线开口向下b与对称轴有关:对称轴为x=-b/2a;c表示抛物线与y轴的交点坐标:(0,c)才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知平行四边形ABCD中,CE平分∠BCD且交AD于点E,A F∥CE,且交BC于点F.
(1)求证:△ABF≌△CDE;
(2)如图,若∠1=65°,求∠B的大小.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某兴趣小组10名学生在一次数学测试中的成绩如表(满分150分)
分数(单位:分)
105
130
140
150
人数(单位:人)
2
4
3
1
下列说法中,不正确的是( )
A.这组数据的众数是130
B.这组数据的中位数是130
C.这组数据的平均数是130
D.这组数据的方差是112.5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,把矩形沿AC折叠,点B落在点E处,AE与DC的交点为O,连接DE.
(1)求证:△ADE≌△CED;
(2)求证:DE∥AC.

-
科目: 来源: 题型:
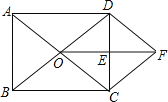
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,对角线AC、BD相交于点O,E是CD中点,连结OE.过点C作CF∥BD交线段OE的延长线于点F,连结DF.求证:
(1)△ODE≌△FCE;
(2)四边形ODFC是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,AD平分∠BAC,AD⊥BC,垂足为D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为E.
(1)求证:四边形ADCE是矩形;
(2)当△ABC满足什么条件时,四边形ADCE是正方形?给出证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=﹣
 x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=
x+m(m>0)与x轴交于点C,与y轴交于点D,以CD为边作矩形ANCD,点A在x轴上.双曲线y=  经过点B,与直线CD交于点E,则点E的坐标为( )
经过点B,与直线CD交于点E,则点E的坐标为( ) 
A.( ,﹣
,﹣  )
)
B.(4,﹣ )
)
C.( ,﹣
,﹣  )
)
D.(6,﹣1)
相关试题

