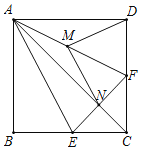
【题目】操作与证明:如图,把一个含![]() 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、![]() 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.
![]() 求证:
求证:![]() 是等腰三角形;
是等腰三角形;
![]() 在
在![]() 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】
(1)根据正方形性质得:AB=AD=BC=CD,∠ABE=∠ADF=90°,再根据等腰直角三角形得BE=DF,证明△ABE≌△ADF,得AE=AF,则△AFE是等腰三角形;
(2)先根据直角三角形斜边中线等于斜边一半得:DM=![]() AF,再由等腰三角形三线合一得:AC⊥EF,EN=FN,同理MN=
AF,再由等腰三角形三线合一得:AC⊥EF,EN=FN,同理MN=![]() AF,则DM=MN;可证∠FMD=2∠FAD,∠FMN==2∠FAC,
AF,则DM=MN;可证∠FMD=2∠FAD,∠FMN==2∠FAC,
则∠DMN=∠DMF+∠FMN=2∠FAD +2∠FAC=2∠DAC=90°.即可得到DM⊥MN.
(1)∵四边形ABCD是正方形,∴AB=AD=BC=CD,∠ABE=∠ADF=90°,
∵△EFC是等腰直角三角形,∴CE=CF,∴BE=DF,∴△ABE≌△ADF(SAS),∴AE=AF,∴△AFE是等腰三角形;
(2)DM=MN,且DM⊥MN.理由是:
在Rt△ADF中,∵M是AF的中点,∴DM=![]() AF,
AF,
∵EC=FC,AC平分∠ECF,
∴AC⊥EF,EN=FN,
∴∠ANF=90°,
∴MN=![]() AF,∴MD=MN.
AF,∴MD=MN.
由(1)得:△ABE≌△ADF,∴∠BAE=∠FAD,
∵DM=![]() AF=AM,∴∠FAD=∠ADM,
AF=AM,∴∠FAD=∠ADM,
∴∠FMD=∠FAD+∠ADM=2∠FAD,
同理:∠FMN==2∠FAC,
∴∠DMN=∠DMF+∠FMN=2∠FAD +2∠FAC=2∠DAC=2×45°=90°.
∴MD⊥MN.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为参加全区的“我爱古诗词”知识竞赛,王晓所在学校组织了一次古诗词知识测试
 王晓从全体学生中随机抽取部分同学的分数
王晓从全体学生中随机抽取部分同学的分数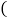 得分取正整数,满分为100分
得分取正整数,满分为100分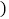 进行统计
进行统计 以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图
以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图 请根据以上频率分布表和布直方图,回答下列问题:
请根据以上频率分布表和布直方图,回答下列问题:组别
分组
频数
频率
1
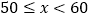
9
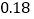
2
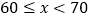
m
b
3
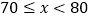
21
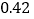
4
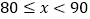
a
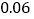
5
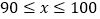
2
n
(1)分别求出a、b、m、n的值;
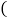 写出计算过程
写出计算过程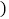
(2)老师说:“王晓的测试成绩是被抽取的同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)得分在
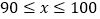 的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?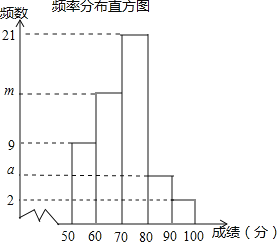
-
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形
 中,
中, ,点E、F分别在边AB、AC上,将
,点E、F分别在边AB、AC上,将 沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且
沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且 .
. 求证:四边形AFDE是菱形.
求证:四边形AFDE是菱形. 若
若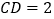 ,
,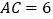 ,求线段ED的长度.
,求线段ED的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8,则AC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分)
中位数(分)
众数(分)
初中部
85
高中部
85
100
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
-
科目: 来源: 题型:
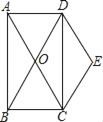
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD交于点O,且DE∥AC,CE∥BD.
(1)求证:四边形OCED是菱形;
(2)若∠BAC=30°,AC=4,求菱形OCED的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
相关试题

