【题目】为参加全区的“我爱古诗词”知识竞赛,王晓所在学校组织了一次古诗词知识测试![]() 王晓从全体学生中随机抽取部分同学的分数
王晓从全体学生中随机抽取部分同学的分数![]() 得分取正整数,满分为100分
得分取正整数,满分为100分![]() 进行统计
进行统计![]() 以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图
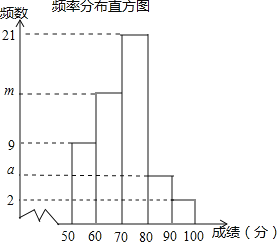
以下是根据这次测试成绩制作的进行统计,以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图![]() 请根据以上频率分布表和布直方图,回答下列问题:
请根据以上频率分布表和布直方图,回答下列问题:
组别 | 分组 | 频数 | 频率 |
1 |
| 9 |
|
2 |
| m | b |
3 |
| 21 |
|
4 |
| a |
|
5 |
| 2 | n |
(1)分别求出a、b、m、n的值;![]() 写出计算过程
写出计算过程![]()
(2)老师说:“王晓的测试成绩是被抽取的同学成绩的中位数”,那么王晓的测试成绩在什么范围内?
(3)得分在![]() 的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
的为“优秀”,若王晓所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加区赛,请问共有多少名学生被选拔参加区赛?
参考答案:
【答案】(1)3,0.04;15;0.3;(2)王晓的测试成绩在![]() 范围内;(3)24人.
范围内;(3)24人.
【解析】
(1)根据频数、频率、总数之间的关系一一解决问题即可;
(2)根据中位数的定义即可判断;
(3)用样本估计总体的思想解决问题即可;
(1)9÷0.18=50(人).
a=60×0.06=3,n=2÷50=0.04,m=50﹣(9+21+3+2)=15,b=15÷50=0.3.
(2)全班共有50名学生,中位数是第25、26个数据的平均数,第25、26个数据在第3组,所以王晓的测试成绩在70≤x<80范围内;
(3)![]() ×600=24(人).
×600=24(人).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某容器由A、B、C三个连通长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是整个容器容积的
 (容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.
(容器各面的厚度忽略不计),A、B的总高度为12厘米.现以均匀的速度(单位:cm3/min)向容器内注水,直到注满为止.已知单独注满A、B分别需要的时间为10分钟、8分钟.(1)求注满整个容器所需的总时间;
(2)设容器A的高度为xcm,则容器B的高度为 cm;
(3)求容器A的高度和注水的速度.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲乙两地相距200千米,一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,相向而行.已知客车的速度为60千米/小时,出租车的速度是100千米/小时.
(1)多长时间后两车相遇?
(2)若甲乙两地之间有相距50km的A、B两个加油站,当客车进入A站加油时,出租车恰好进入B站加油,求A加油站到甲地的距离.
(3)若出租车到达甲地休息10分钟后,按原速原路返回.出租车能否在到达乙地或到达乙地之前追上客车?若不能,则出租车往返的过程中,至少提速为多少才能在到达乙地或到达乙地之前追上客车?是否超速(高速限速为120千米/小时)?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AC为对角线,点E在AB边上,EF⊥AC于点F,连接EC,AF=3,△EFC的周长为12,则EC的长为( )

A.
B.3
C.5
D.6 -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角三角形
 中,
中, ,点E、F分别在边AB、AC上,将
,点E、F分别在边AB、AC上,将 沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且
沿着直线EF折叠,使得A点恰好落在BC边上的D点处,且 .
. 求证:四边形AFDE是菱形.
求证:四边形AFDE是菱形. 若
若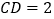 ,
,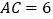 ,求线段ED的长度.
,求线段ED的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知⊙O的直径CD=10,AB是⊙O的弦,AB⊥CD,垂足为M,且AB=8,则AC的长为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】操作与证明:如图,把一个含
 角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、
角的直角三角板ECF和一个正方形ABCD摆放在一起,使三角板的直角顶点和正方形的顶点C重合,点E、F分别在正方形的边CB、CD上,连接AC、AE、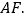 其中AC与EF交于点N,取AF中点M,连接MD、MN.
其中AC与EF交于点N,取AF中点M,连接MD、MN.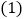 求证:
求证: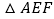 是等腰三角形;
是等腰三角形;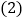 在
在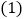 的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.
的条件下,请判断MD,MN的数量关系和位置关系,并给出证明.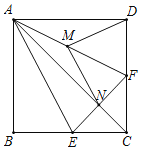
相关试题

