【题目】如图,在△ABC中,AB=AC,点D、E、F分别在BC、AB、AC边上,且BE=CF, BD=CE.

(1)求证:△DEF是等腰三角形;
(2)当∠A=40°时,求∠DEF的度数;
(3)△DEF可能是等腰直角三角形吗?为什么?
参考答案:
【答案】(1)证明见试题解析;(2)70°;(3)不可能,理由见试题解析.
【解析】试题分析:(1)根据AD+EC=AB=AD+DB得出EC=DB,根据AB=AC得出∠B=∠C,结合BE=CF得出△BED和△ECF全等,从而得出答案;(2)根据∠A的度数以及等腰三角形的性质得出∠B和∠C的度数,根据三角形全等得出∠DEF的度数;(3)当△DEF为等腰直角三角形时则∠DEF=90°,从而得出∠DEB+∠BDE=90°,则∠B=90°,得出与三角形内角和为180°相矛盾得出答案.
试题解析:(1)∵AD+EC=AB=AD+DB,∴EC=DB.
又AB=AC
∴∠B=∠C
又BE=CF
∴△BED≌△ECF
∴DE=EF
∴△DEF是等腰三角形
(2)∵∠A=40°∴∠B=∠C=70°由(1)知∠BDE=∠FEC
∴∠DEF=∠B=70°
(3)若△DEF是等腰直角三角形,则∠DEF=90°
∴∠DEB+∠BDE=90°,
∴∠B=90°因而∠C=90°
∴△DEF不可能是等腰直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.

(1)求证:CD为⊙O的切线;
(2)若CD=2AD,⊙O的直径为10,求线段AB的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 是
是 的直径,
的直径, .
.(1)求证:
 是
是 的切线;
的切线;(2)若点
 是
是 的中点,连接
的中点,连接 交
交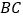 于点
于点 ,当
,当 ,
, 时,求
时,求 的值.
的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组做“用频率估计概率”的试验时,统计了某一结果出现的频率,绘制了如图所示的折线统计图,则符合这一结果的试验最有可能的是( )

A. 在“石头、剪刀、布”的游戏中,小明随机出的是“剪刀”
B. 一副去掉大小王的普通扑克牌洗匀后,从中任抽一张牌的花色是红桃
C. 暗箱中有1个红球和2个黄球,它们只有颜色上的区别,从中任取一球是黄球
D. 掷一个质地均匀的正六面体骰子,向上的面点数是4
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场销售A、B两种品牌的教学设备,这两种教学设备的进价和售价如下表所示:
教学设备
A
B
进价(万元/套)
3
2.4
售价(万元/套)
3.3
2.8
该商场计划购进两种教学设备若干套,共需132万元,全部销售后可获毛利润18万元.
(1)该商场计划购进A、B两种品牌的教学设备各多少套?
(2)通过市场调查,该商场决定在原计划的基础上,减少A种设备的购进数量,增加B种设备的购进数量,已知B种设备增加的数量是A种设备减少数量的1.5倍.若用于购进这两种教学设备的总资金不超过138万元,则A种设备购进数量最多减少多少套?
-
科目: 来源: 题型:
查看答案和解析>>【题目】课外阅读是提高学生素养的重要途径,某校为了了解学生课外阅读情况,随机抽查了50名学生,统计他们平均每天课外阅读时间(t小时),根据t的长短分为A,B,C,D四类.下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:

(1)求表格中的a值,并在图中补全条形统计图;
(2)该校现有1300名学生,请你估计该校共有多少学生课外阅读时间不少于1小时.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠BAC=30°,AM是∠BAC的平分线,过M作ME∥BA交AC于E,作MD⊥BA,垂足为D,ME=10cm,则MD=_________.

相关试题

