Question

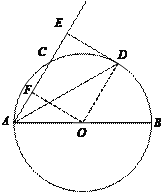
【题目】如图，AB是⊙O的直径，AC与⊙O交于点C，∠BAC的平分线交⊙O于点D，DE⊥AC，垂足为E．

（1）求证：DE是⊙O的切线；

（2）若直径AB＝10，弦AC＝6，求DE的长．

Answer 1

【答案】（1）见解析；（2）4．

【解析】试题分析： 连结OD，∵AD平分∠BAC，∠OAD＝∠CAD，∵OA＝OD，

∴∠OAD＝∠ODA，∴∠ODA＝∠CAD，得出OD∥AC，得到∠ODE＝90°，从而得证.

在Rt△AFO中，利用勾股定理：AF2＋OF2＝AO2，得出的长，四边形ODEF是矩形，从而得到的长.

试题解析： 连结OD．

∵AD平分∠BAC，

∴∠OAD＝∠CAD，

∵OA＝OD，

∴∠OAD＝∠ODA，

∴∠ODA＝∠CAD，

∴OD∥AC，

∵DE⊥AC，

即∠AED＝90°，

∴∠ODE＝90°，

即DE⊥OD．

∴DE是⊙O的切线．

（2）解：作OF⊥AC，垂足为F．

在Rt△AFO中，AF2＋OF2＝AO2，

∴32＋OF2＝52，

∴ OF＝4，

∵∠AED＝∠ODE＝∠OFE＝90°，

∴四边形ODEF是矩形，

∴DE＝OF＝4．