搜索
【题目】如图，在△ABC中，AC=BC，点D，E分别是边AB，AC的中点，延长DE至点F，使EF=DE，则四边形ADCF一定是（ ）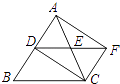 
A.矩形
B.菱形
C.正方形
D.梯形
参考答案：
【答案】A
【解析】解：∵E是AC中点， ∴AE=EC，
∵DE=EF，
∴四边形ADCF是平行四边形，
∵AD=DB，AE=EC，
∴DE= 
BC，
∴DF=BC，
∵CA=CB，
∴AC=DF，
∴四边形ADCF是矩形；
故选：A．
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识，掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形，以及对矩形的判定方法的理解，了解有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，为了对一颗倾斜的古杉树AB进行保护，需测量其长度：在地面上选取一点C，测得∠ACB=45°，AC=24m，∠BAC=66.5°，（参考数据：
≈1.414，sin66.5°≈0.92，cos66.5°≈0.40，tan66.5°≈2.30）．则这颗古杉树AB的长约为（ ） 
A.7.27
B.16.70
C.17.70
D.18.18 -
科目： 来源： 题型：
查看答案和解析>>【题目】画图并填空，如图：方格纸中每个小正方形的边长都为1，△ABC的顶点都在方格纸的格点上，将△ABC经过一次平移后得到△A'B'C'．图中标出了点C的对应点C'．
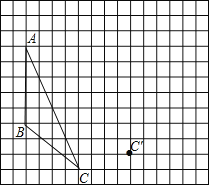
（1）请画出平移后的△A'B'C'；
（2）若连接AA'，BB'，则这两条线段的关系是 ；
（3）利用网格画出△ABC中AC边上的中线BD以及AB边上的高CE；
（4）线段AB在平移过程中扫过区域的面积为 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知，如图，在△ABC中，∠A=∠ABC，直线EF分别交△ABC的边AB，AC和CB的延长线于点D，E，F．
（1）求证：∠F+∠FEC=2∠A；
（2）过B点作BM∥AC交FD于点M，试探究∠MBC与∠F+∠FEC的数量关系，并证明你的结论．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，为厉行节能减排，倡导绿色出行，某公司拟在我市甲、乙两个街道社区投放一批共享单车（俗称“小黄车”），这批自行车包括A、B两种不同款型．
成本单价 （单位：元）
投放数量
（单位：辆）
总价（单位：元）
A型
x
50
50x
B型
x+10
50
成本合计（单位：元）
7500
问题1：看表填空
如图2所示，本次试点投放的A、B型“小黄车”共有 辆；用含有x的式子表示出B型自行车的成本总价为 ；
问题2：自行车单价
试求A、B两型自行车的单价各是多少？
问题3：投放数量
现在该公司采取如下方式投放A型“小黄车”：甲街区每100人投放n辆，乙街区每100人投放（n+2）辆，按照这种投放方式，甲街区共投放1500辆，乙街区共投放1200辆，如果两个街区共有
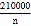人，求甲街区每100人投放A型“小黄车”的数量．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将一副三角板按如图摆放，其中△ABC为含有45度角的三角板，直线AD是等腰直角三角形ABC的对称轴，且将△ABC分成两个等腰直角三角形，DM、DN分别与边AB、AC交于E、F两点，有下列四个结论：①BD＝AD＝CD②△AED≌△CFD③BE+CF＝EF④S四边形AEDF＝
AB2．其中正确结论是_____（填写正确序号）
-
科目： 来源： 题型：
查看答案和解析>>【题目】某公司有
、
两种型号的客车共20辆，它们的载客量、每天的租金如下表所示.已知在20辆客车都坐满的情况下，共载客720人.A型号客车
B型号客车
载客量(人/辆)
45
30
租金(元/辆)
600
450
(1)求
、两种型号的客车各有多少辆?(2)某中学计划租用
、两种型号的客车共8辆，同时送七年级师生到沙家浜参加社会实践活动，已知该中学租车的总费用不超过4600元. 求最多能租用多少辆A型号客车？
相关试题
