搜索
【题目】甲、乙两辆汽车分别从A、B两城同时沿高速公路驶向C城．已知A、C两城的路程为500千米，B、C两城的路程为450千米，甲车比乙车的速度快10千米／时，结果两辆车同时到达C城，求两车的速度．
参考答案：
【答案】甲车的速度为100千米/时，乙车的速度为90千米/时.
【解析】试题分析：设甲的速度是x千米/时，那么乙的速度是（x-10）千米/时，路程知道，且同时到达，可以时间做为等量关系列方程求解．
试题解析：设乙车的速度为x千米/时，则甲车的速度为（x+10）千米/时.
根据题意，得
.
解得x=90.
经检验，x=90是原方程的解，且符合题意.
当x=90时，x+10=100.
答：甲车的速度为100千米/时，乙车的速度为90千米/时.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在大课间活动中，同学们积极参加体育锻炼，小龙在全校随机抽取了一部分同学就“我最喜爱的体育项目”进行了一次调查（每位同学必选且只选一项）．下面是他通过收集的数据绘制的两幅不完整的统计图，请你根据图中提供的信息，解答以下问题：
（1）小龙一共抽取了 名学生．
（2）补全条形统计图；
（3）求“其他”部分对应的扇形圆心角的度数．
-
科目： 来源： 题型：
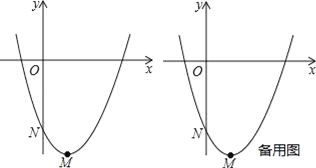
查看答案和解析>>【题目】已知抛物线l：y=ax2+bx+c（a，b，c均不为0）的顶点为M，与y轴的交点为N，我们称以N为顶点，对称轴是y轴且过点M的抛物线为抛物线l的衍生抛物线，直线MN为抛物线l的衍生直线．
（1）如图，抛物线y=x2﹣2x﹣3的衍生抛物线的解析式是 ，衍生直线的解析式是 ；
（2）若一条抛物线的衍生抛物线和衍生直线分别是y=﹣2x2+1和y=﹣2x+1，求这条抛物线的解析式；
（3）如图，设（1）中的抛物线y=x2﹣2x﹣3的顶点为M，与y轴交点为N，将它的衍生直线MN先绕点N旋转到与x轴平行，再沿y轴向上平移1个单位得直线n，P是直线n上的动点，是否存在点P，使△POM为直角三角形？若存在，求出所有点P的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】要使式子9x2+25y2成为一个完全平方式，则需加上（ ）
A.15xy
B.±15xy
C.30xy
D.±30xy -
科目： 来源： 题型：
查看答案和解析>>【题目】公元前6世纪古希腊的毕达哥拉斯学派有一种观点，即“万物皆数”，一切量都可以用整数或整数比（分数）表示，后来，当这一学派中的希帕索斯发现，边长为1的正方形的对角线的长度不能用整数或整数的比表示时，毕达哥拉斯学派感到惊恐不安，由此，引发了第一次数学危机，这儿“不能用整数或整数的比表示的数”指的是（ ）
A.有理数B.无理数C.合数D.质数
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：二次函数y=x2+bx+3的图象经过点(3，0).
（1）求b的值；
（2）求出该二次函数图象的顶点坐标和对称轴；
（3）在所给坐标系中画出二次函数y=x2+bx+3的图象.
-
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，∠BAC=90
，AB=AC.点D为直线BC上一动点（点D不与点B、C重合），以AD为直角边在AD右侧作等腰直角三角形ADE，使
DAE=90
，连结CE.探究：如图①，当点D在线段BC上时，证明BC=CE+CD.
应用：在探究的条件下，若AB=
，CD=1，则△DCE的周长为_______.拓展：(1)如图②，当点D在线段CB的延长线上时，BC、CD、CE之间的数量关系为_______.
(2)如图③，当点D在线段BC的延长线上时，BC、CD、CE之间的数量关系为_______.
相关试题
