搜索
【题目】如图，小红用一张长方形纸片ABCD进行折纸，已知该纸片宽AB为8cm，长BC为10cm．当小红折叠时，顶点D落在BC边上的点F处（折痕为AE）．此时EC有多长？
参考答案：
【答案】3
【解析】试题分析：根据题意，在Rt△FCE中，利用勾股定理求出EC长，设EC为x，因为△ADE与△AFE对折，所以 EF=DE=8-x， AF=AD=10， 在Rt△ABF中，利用勾股定理能求出BF=6，所以FC=4， 在Rt△FCE中， 利用勾股定理可求出EC．
试题解析：根据题意，设EC为x ，∵△ADE与△AFE对折，
∴EF=DE=8-x，Rt△ABF中，AF=AD=10，AB=8，BF2=AF2-AB2，
∴BF=6，∴FC=BC-BF=10-6=4，在Rt△FCE中，EC=x，EF=8-x，FC=4，
∴（8-x）2=x2+42，解得：x=3，即EC=3．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，
，BE平分
，
．
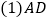与BC平行吗？请说明理由；
与EF的位置关系如何？为什么？解：
理由如下：
平角的定义
已知
______
______
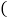______与EF的位置关系是______
平分
已知
角平分线的定义又
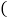，已知即
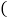______等量代换
______
______
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x1 ， 0），C（x2 ， 0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y轴的直线l与抛物线、直线AD的交点分别为P、Q．
（1）求抛物线的解析式；
（2）当0＜t≤8时，求△APC面积的最大值；
（3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由． -
科目： 来源： 题型：
查看答案和解析>>【题目】在△ABC中，BC=AC，∠BCA=90°，P为直线AC上一点，过点A作AD⊥BP于点D，交直线BC于点Q．
（1）如图1，当P在线段AC上时，求证：BP=AQ；
（2）如图2，当P在线段CA的延长线上时，（1）中的结论是否成立？ （填“成立”或“不成立”）
（3）在（2）的条件下，当∠DBA= 度时，存在AQ=2BD，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某化妆品店老板到厂家选购A、B两种品牌的化妆品，若购进A品牌的化妆品5套，B品牌的化妆品6套，需要950元；若购进A品牌的化妆品3套，B品牌的化妆品2套，需要450元．
求A、B两种品牌的化妆品每套进价分别为多少元？
若销售1套A品牌的化妆品可获利30元，销售1套B品牌的化妆品可获利20元，根据市场需求，化妆品店老板决定，购进B品牌化妆品的数量比购进A品牌化妆品数量的2倍还多4套，且B品牌化妆品最多可购进40套，这样化妆品全部售出后，可使总的获利不少于1200元，问有几种进货方案？如何进货？ -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD内接于⊙O，点E在劣弧AD上，则∠BEC等于（ ）
A.45°
B.60°
C.30°
D.55° -
科目： 来源： 题型：
查看答案和解析>>【题目】已知：
，OE平分
，点A、B、C分别是射线OM、OE、ON上的动点
、B、C不与点O重合
，连接AC交射线OE于点
设
．
如图1，若
，则
的度数是______；
当
时，
______；当
时，______．
如图2，若
，则是否存在这样的x的值，使得
中有两个相等的角？若存在，求出x的值；若不存在，说明理由．
相关试题
