【题目】某教育局为了解七年级学生一个学期参加综合实践活动的情况,随机抽样调查了某校七年级学生一个学期参加综合实践活动的天数,并用得到的数据绘制了下面两幅不完整的统计图(如图),请你根据图中提供的信息,回答下列问题:
(1)求出该校七年级学生总数;
(2)在这次抽样调查中,众数和中位数分别是多少?


参考答案:
【答案】(1)总人数为200人;(2)众数是4天,中位数是4天.
【解析】
(1)由参加实践活动为2天的人数除以所占的百分比即可求出八年级学生总数;
(2)出现次数最多的天数为4天,故众数为4;将实践活动的天数按照从小到大顺序排列,找出最中间的两个天数,求出平均数即可得到中位数;
(1)总人数为20÷10%=200(人);
(2)∵a=1-30%-15%-10%-5%-15%=25%,
∴活动时间为5天的七年级学生人数为200×25%=50(人).
活动时间为7天的七年级学生人数为200×5%=10(人),
由图中的数据可知,4天出现60次,次数最多,所以众数是4天;
数据按从小到大顺序排列,中位数是4天.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知a是最大的负整数,b是5的相反数,c=|2|,且a、b、c分别是点A. B.C在数轴上对应的数.
(1)求a、b、c的值,并在数轴上标出点A. B. C.
(2)若动点P从点A出发沿数轴正方向运动,动点Q同时从点B出发也沿数轴正方向运动,点P的速度是每秒3个单位长度,点Q的速度是每秒1个单位长度,求运动几秒后,点Q可以追上点P?
(3)在数轴上找一点M,使点M到A. B.C三点的距离之和等于12,请直接写出所有点M对应的数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
(1)已知:如图1,在正方形ABCD中,点E、H分别在BC、AB上,若AE⊥DH于点O,求证AE=DH;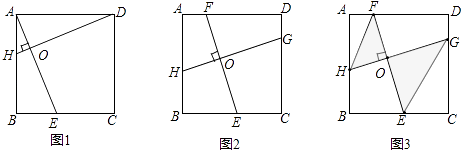
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
拓展应用:
(3)已知,如图3,在(2)问条件下,若BC=4,E为BC的中点,AF= AD,求HG的长
AD,求HG的长 -
科目: 来源: 题型:
查看答案和解析>>【题目】两个一次函数
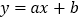 和
和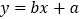 的图象在同一坐标系内大致位置正确的是( )
的图象在同一坐标系内大致位置正确的是( )A.
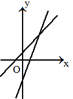 B.
B. 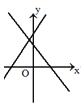 C.
C. 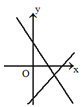 D.
D. 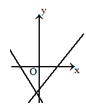
-
科目: 来源: 题型:
查看答案和解析>>【题目】“国美”、“苏宁”两家电器商场出售同样的空气净化器和过滤网,空气净化器和过滤网在两家商场的售价一样.已知买一个空气净化器和
 个过滤网要花费
个过滤网要花费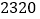 元,买
元,买 个空气净化器和
个空气净化器和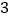 个过滤网要花费
个过滤网要花费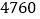 元.
元.(
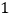 )请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?
)请用方程组求出一个空气净化器与一个过滤网的销售价格分别是多少元?(
 )为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买
)为了迎接新年,两家商场都在搞促销活动,“国美”规定:这两种商品都打九五折;“苏宁”规定:买一个空气净化器赠送两个过滤网.若某单位想要买 个空气净化器和
个空气净化器和 个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由.
个过滤网,如果只能在一家商场购买,请问选择哪家商场购买更合算?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图信息,L1为走私船,L2为我公安快艇,航行时路程与时间的函数图象,问

(1)在刚出发时我公安快艇距走私船多少海里?
(2)计算走私船与公安快艇的速度分别是多少?
(3)写出L1,L2的解析式
(4)问6分钟时两艇相距几海里.
(5)猜想,公安快艇能否追上走私船,若能追上,那么在几分钟追上?
-
科目: 来源: 题型:
查看答案和解析>>【题目】请认真观察图形,解答下列问题:
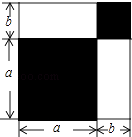
(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);
(2)由(1),你能得到怎样的等量关系?请用等式表示;
(3)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a4﹣b4的值.
相关试题

