搜索
【题目】在正方形网格中，每个小正方形的边长均为1个单位长度，△ABC的三个顶点的位置如图所示．现将△ABC平移，使点A变换为点D，点E、F分别是B、C的对应点．
（1）请画出平移后的△DEF；
（2）若连接AD、CF，则这两条线段之间的关系是________________；
（3）在图中找出所有满足S△ABC＝S△QBC的格点Q (异于点A)，并用Q1、Q2…表示．
参考答案：
【答案】AD=CF，AD∥CF
【解析】分析：（1）根据网格结构找出点B、C平移后的对应点E、F的位置，然后与点D顺次连接即可；
（2）根据平移的性质，对应点的连线平行且相等；
（3）过点A作线段BC的平行线，平行线经过的网格点即为点Q1、Q2．．
详解：（1）如图所示；
（2）AD与CF平行且相等．
故答案为：AD与CF平行且相等．
（3）过点A作线段BC的平行线，平行线经过的网格点即为点Q1、Q2．，如图，
-
科目： 来源： 题型：
查看答案和解析>>【题目】【知识生成】我们已经知道，通过计算几何图形的面积可以表示一些代数恒等式.
例如图
可以得到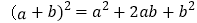
，基于此，请解答下列问题：（1）根据图2，写出一个代数恒等式： ．
(2)利用（1）中得到的结论，解决下面的问题：若a+b+c=10，ab+ac+bc=35，
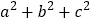= .(3) 小明同学用图 中x 张边长为a 的正方形， y张边长为b 的正方形，z 张宽、长分别为 a、b 的长方形纸片拼出一个面积为 (2a+b)(a+2b)长方形，则x+y+z=
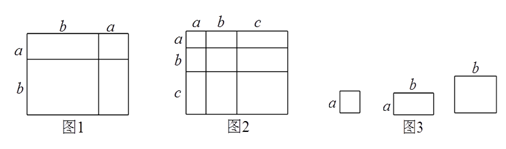
【知识迁移】（4）事实上，通过计算几何图形的体积也可以表示一些代数恒等式，图4表示的是一个边长为
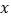的正方体挖去一个小长方体后重新拼成一个新长方体，请你根据图4中图形的变化关系，写出一个代数恒等式： ．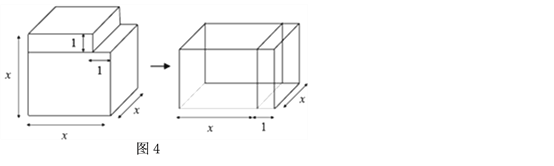
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知在四边形
中，∠A=∠C=90°．（1）如图1，若BE平分∠ABC，DF平分∠ADC的邻补角，请写出BE与DF的位置关系，并证明．
（2）如图2，若BF、DE分别平分∠ABC、∠ADC的邻补角，判断DE与BF位置关系并证明．
（3）如图3，若BE、DE分别五等分∠ABC、∠ADC的邻补角（即∠CDE=
，∠CBE=
），则∠E= ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，要得到AB∥CD，只需要添加一个条件，这个条件不可以是（ ）
A. ∠1＝∠3 B. ∠B＋∠BCD＝180°
C. ∠2＝∠4 D. ∠D＋∠BAD＝180°
-
科目： 来源： 题型：
查看答案和解析>>【题目】某校组织“大手拉小手，义卖献爱心”活动，计划购买黑白两种颜色的文化衫进行手绘设计后出售，并将所获利润全部捐给山区困难孩子．已知该学校从批发市场花3600元购买了黑白两种颜色的文化衫200件．每件文化衫的批发价及手绘后的零售价如下表：
批发价（元）
零售价（元）
黑色文化衫
20
35
白色文化衫
15
25
假设通过手绘设计后全部售出，求该校这次义卖活动所获利润．
-
科目： 来源： 题型：
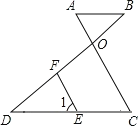
查看答案和解析>>【题目】如图,AB∥DC，AC和BD相交于点O，E是CD上一点，F是OD上一点，且∠1=∠A.
(1)求证：FE∥OC；
(2)若∠BOC比∠DFE大20，求∠OFE的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】画图并填空：如图，每个小正方形的边长为1个单位，每个小正方形的顶点叫格点.
（1）将△ABC向左平移8格，再向下平移1格．请在图中画出平移后的△A′B′C′
（2）利用网格在图中画出△ABC的中线CD，高线AE；
（3）△A′B′C′的面积为_____．
（4）在平移过程中线段BC所扫过的面积为 .
（5）在右图中能使
的格点P的个数有 个(点P异于A).
相关试题
