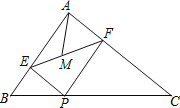
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .
参考答案:
【答案】![]()
【解析】
试题分析:根据矩形的性质就可以得出EF,AP互相平分,且EF=AP,根据垂线段最短的性质就可以得出AP⊥BC时,AP的值最小,即AM的值最小,由勾股定理求出BC,根据面积关系建立等式求出其解即可.
解:∵PE⊥AB,PF⊥AC,∠BAC=90°,
∴∠EAF=∠AEP=∠AFP=90°,
∴四边形AEPF是矩形,
∴EF,AP互相平分.且EF=AP,
∴EF,AP的交点就是M点,
∵当AP的值最小时,AM的值就最小,
∴当AP⊥BC时,AP的值最小,即AM的值最小.
∵![]() AP×BC=
AP×BC=![]() AB×AC,
AB×AC,
∴AP×BC=AB×AC,
在Rt△ABC中,由勾股定理,得BC=![]() =10,
=10,
∵AB=6,AC=8,
∴10AP=6×8,
∴AP=![]()
∴AM=![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某个商贩同时卖出两件上衣,售价都是135元,按成本计算,其中一件盈利25%,另一件亏损25%,在这次交易中,该商贩( )
A. 不赔不赚 B. 赚9元 C. 赔9元 D. 赔18元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根,则a的值是( )
A.4
B.-4
C.1
D.-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个共一个顶点的等腰直角△ABC和等腰直角△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
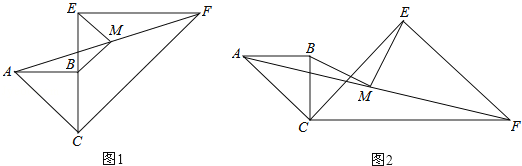
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC内接于⊙O,∠BAC=120°,AB=AC ,BD为⊙O的直径,AD=6 ,求BC的长

-
科目: 来源: 题型:
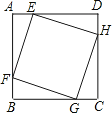
查看答案和解析>>【题目】如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=﹣6x+5的图象是由直线y=﹣6x向_____平移_____个单位长度得到的.
相关试题

