【题目】已知两个共一个顶点的等腰直角△ABC和等腰直角△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
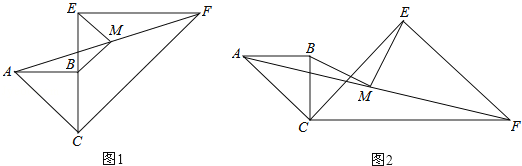
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
参考答案:
【答案】(1)见解析(2)BM=ME==![]() a(3)见解析
a(3)见解析
【解析】
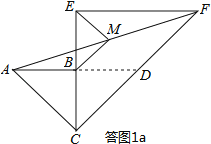
试题分析:(1)如答图1a所示,延长AB交CF于点D,证明BM为△ADF的中位线即可;
(2)如答图2a所示,作辅助线,推出BM、ME是两条中位线;
(3)如答图3a所示,作辅助线,推出BM、ME是两条中位线:BM=![]() DF,ME=
DF,ME=![]() AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
AG;然后证明△ACG≌△DCF,得到DF=AG,从而证明BM=ME.
(1)证明:如答图1a,延长AB交CF于点D,则易知△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD,
∴点B为线段AD的中点,
又∵点M为线段AF的中点,
∴BM为△ADF的中位线,
∴BM∥CF;
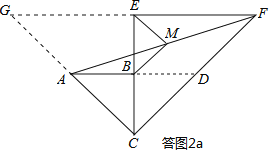
(2)如答图2a所示,延长AB交CF于点D,则易知△BCD与△ABC为等腰直角三角形,
∴AB=BC=BD=a,AC=CD=![]() a,
a,
∴点B为AD中点,又点M为AF中点,
∴BM=![]() DF.
DF.
分别延长FE与CA交于点G,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=GE=2a,CG=CF=2![]() a,
a,
∴点E为FG中点,又点M为AF中点,
∴ME=![]() AG.
AG.
∵CG=CF=2![]() a,CA=CD=
a,CA=CD=![]() a,
a,
∴AG=DF=![]() a,
a,
∴BM=ME=![]() ×
×![]() a=
a=![]() a.
a.
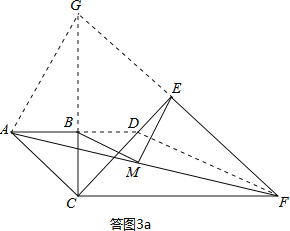
(3)如答图3a,延长AB交CE于点D,连接DF,则易知△ABC与△BCD均为等腰直角三角形,
∴AB=BC=BD,AC=CD,
∴点B为AD中点,又点M为AF中点,
∴BM=![]() DF,
DF,
延长FE与CB交于点G,连接AG,则易知△CEF与△CEG均为等腰直角三角形,
∴CE=EF=EG,CF=CG,
∴点E为FG中点,又点M为AF中点,
∴ME=![]() AG,
AG,
在△ACG与△DCF中,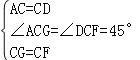 ,
,
∴△ACG≌△DCF(SAS),
∴DF=AG,
∴BM=ME.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某药品说明书上标明药品保存的温度是(10±4)℃,设该药品合适的保存温度为t,则温度t的范围是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某个商贩同时卖出两件上衣,售价都是135元,按成本计算,其中一件盈利25%,另一件亏损25%,在这次交易中,该商贩( )
A. 不赔不赚 B. 赚9元 C. 赔9元 D. 赔18元
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根,则a的值是( )
A.4
B.-4
C.1
D.-1 -
科目: 来源: 题型:
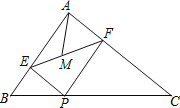
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,△ABC内接于⊙O,∠BAC=120°,AB=AC ,BD为⊙O的直径,AD=6 ,求BC的长

-
科目: 来源: 题型:
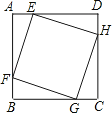
查看答案和解析>>【题目】如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为 .
相关试题

