【题目】已知,如图,△ABC内接于⊙O,∠BAC=120°,AB=AC ,BD为⊙O的直径,AD=6 ,求BC的长

参考答案:
【答案】6.
【解析】
试题分析:首先过点O作OF⊥BC于F,由垂径定理可得BF=CF=![]() BC,然后由∠BAC=120°,AB=AC,利用等边对等角与三角形内角和定理,即可求得∠C与∠BAC的度数,由BD为⊙O的直径,即可求得∠BAD与∠D的度数,又由AD=6,即可求得BD的长,继而求得BC的长.
BC,然后由∠BAC=120°,AB=AC,利用等边对等角与三角形内角和定理,即可求得∠C与∠BAC的度数,由BD为⊙O的直径,即可求得∠BAD与∠D的度数,又由AD=6,即可求得BD的长,继而求得BC的长.
试题解析:过点O作OF⊥BC于F,

∴BF=CF=![]() BC,
BC,
∵AB=AC,∠BAC=120°,
∴∠C=∠ABC=![]() =30°,
=30°,
∵∠C与∠D是![]() 对的圆周角,
对的圆周角,
∴∠D=∠C=30°,
∵BD为⊙O的直径,
∴∠BAD=90°,
∴∠ABD=60°,
∴∠OBC=∠ABD-∠ABC=30°,
∵AD=6,
∴BD=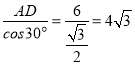 ,
,
∴OB=![]() BD=2
BD=2![]() ,
,
∴BF=OB×cos30°=2![]() ×
×![]() =3,
=3,
∴BC=6.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+2x-a=0有两个相等的实数根,则a的值是( )
A.4
B.-4
C.1
D.-1 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知两个共一个顶点的等腰直角△ABC和等腰直角△CEF,∠ABC=∠CEF=90°,连接AF,M是AF的中点,连接MB、ME.
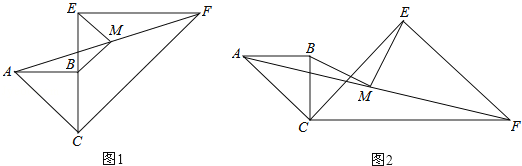
(1)如图1,当CB与CE在同一直线上时,求证:MB∥CF;
(2)如图1,若CB=a,CE=2a,求BM,ME的长;
(3)如图2,当∠BCE=45°时,求证:BM=ME.
-
科目: 来源: 题型:
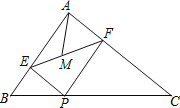
查看答案和解析>>【题目】如图,在Rt△ABC中,∠BAC=90°,AB=6,AC=8,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF中点,则AM的最小值是 .
-
科目: 来源: 题型:
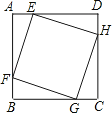
查看答案和解析>>【题目】如图,已知:正方形EFGH的顶点E、F、G、H分别在正方形ABCD的边DA、AB、BC、CD上.若正方形ABCD的面积为16,AE=1,则正方形EFGH的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】函数y=﹣6x+5的图象是由直线y=﹣6x向_____平移_____个单位长度得到的.
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简:
①3x2+2x-5x2+3x ②(a2+2ab+b2)+2(a2-ab-3b2)
相关试题

