【题目】如图,直线AB∥CD,∠B=∠D=120°,E,F在AB上,且∠1=∠2,∠3=∠4
(1)求证:AD∥BC;
(2)求∠ACE的度数;
(3)若平行移动AD,那么∠CAF:∠CFE的值是否发生变化?若变化,找出变化规律或求出其变化范围;若不变,求出这个比值. 
参考答案:
【答案】
(1)解:∵AB∥CD,
∴∠B+∠BCD=180°,
∵∠B=∠D=120°,
∴∠BCD=60°,且∠D+∠BCD=180°,
∴AD∥BC
(2)解:∵∠1=∠2,∠3=∠4,
∴∠ACE=∠2+∠3= ![]() (∠1+∠2)+
(∠1+∠2)+ ![]() (∠3+∠4)=
(∠3+∠4)= ![]() (∠1+∠2+∠3+∠4)=
(∠1+∠2+∠3+∠4)= ![]() ∠BCD=
∠BCD= ![]() ×60°=30°
×60°=30°
(3)解:不变.
∵AB∥CD,
∴∠CAF=∠1,∠CFE=∠1+∠2,
∴∠CAF:∠CFE=∠1:(∠1+∠2)=∠1:2∠1= ![]() ,
,
即这两个角的比值是 ![]()
【解析】(1)根据平行线的性质推出∠B+∠BCD=180°,由∠B=∠D证得∠D+∠BCD=180°,根据平行线的判定即可证得结论;(2)根据平行线的性质推出∠B+∠BCD=180°,由∠B=∠D=120°得到∠BCD=60°,由∠1=∠2,∠3=∠4得到∠ACE= ![]() (∠1+∠2+∠3+∠4)=
(∠1+∠2+∠3+∠4)= ![]() ∠BCD,代入数值即可求得结论;(3)根据平行线的性质证得∠CAF=∠1,∠CFE=∠1+∠2=2∠1,代入即可求出结论.
∠BCD,代入数值即可求得结论;(3)根据平行线的性质证得∠CAF=∠1,∠CFE=∠1+∠2=2∠1,代入即可求出结论.
【考点精析】解答此题的关键在于理解垂线的性质的相关知识,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短,以及对平行线的判定的理解,了解同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒
 ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.

(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6),过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程x2﹣(2m﹣1)x+m2﹣m﹣2=0.
⑴不解方程,判别方程根的情况;
⑵若方程有一个根为1,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,把一块含45°角的三角板的直角顶点靠在长尺(两边a∥b)的一边b上,若∠1=30°,则三角板的斜边与长尺的另一边a的夹角∠2的度数为( )
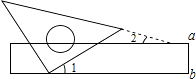
A.10°
B.15°
C.30°
D.35° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字 ,
, ,
, ,
, ,如图
,如图 ,正方形
,正方形 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图 起跳,第一次掷得
起跳,第一次掷得 ,就顺时针连续跳
,就顺时针连续跳 个边长,落到圈
个边长,落到圈 ;若第二次掷得
;若第二次掷得 ,就从
,就从 开始顺时针连续跳
开始顺时针连续跳 个边长,落到圈
个边长,落到圈 ;
; 设游戏者从圈
设游戏者从圈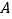 起跳.
起跳.(
 )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈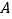 的概率
的概率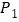 .
.(
 )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈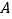 的概率
的概率 ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈 的可能性一样吗?
的可能性一样吗?
相关试题

