【题目】如图1,在Rt△ABC中,∠C=90°,BC=8厘米,点D在AC上,CD=3厘米.点P、Q分别由A、C两点同时出发,点P沿AC方向向点C匀速移动,速度为每秒k厘米,行完AC全程用时8秒;点Q沿CB方向向点B匀速移动,速度为每秒1厘米.设运动的时间为x秒![]() ,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.
,△DCQ的面积为y1平方厘米,△PCQ的面积为y2平方厘米.


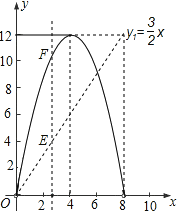
(1)求y1与x的函数关系,并在图2中画出y1的图象;
(2)如图2,y2的图象是抛物线的一部分,其顶点坐标是(4,12),求点P的速度及AC的长;
(3)在图2中,点G是x轴正半轴上一点(0<OG<6),过G作EF垂直于x轴,分别交y1、y2于点E、F.
①说出线段EF的长在图1中所表示的实际意义;
②当0<x<6时,求线段EF长的最大值.
参考答案:
【答案】(1)![]() .图象如图所示:
.图象如图所示:
(2)点P的速度每秒![]() 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①表示△PCQ与△DCQ的面积差(或△PDQ面积);②![]()
【解析】
试题分析:(1)已知了CD=3,根据Q点的速度可以用时间x表示出CQ的长,可根据三角形的面积计算公式得出y1,x的函数关系式;
(2)可先求出y2的函数式,然后根据其顶点坐标来确定k的取值.已知了P点走完AC用时8s,因此AC=8k,而AP=kx,CQ=x,那么可根据三角形的面积公式列出关于y2,x的函数关系式,进而可根据顶点坐标求出k的值;
(3)EF其实就是y2-y1,也就是三角形PCQ和CDQ的面积差即三角形PDQ的面积.得出EF的函数关系式后,根据自变量的取值以及函数的性质即可求出EF的最大值.
(1)∵![]() ,CD=3,CQ=x,
,CD=3,CQ=x,
∴![]() .图象如图所示:
.图象如图所示:

(2)![]() ,CP=8k-xk,CQ=x,
,CP=8k-xk,CQ=x,
∴![]() .
.
∵抛物线顶点坐标是(4,12),
∴![]() .解得
.解得![]()
则点P的速度每秒![]() 厘米,AC=12厘米;
厘米,AC=12厘米;
(3)①观察图象,知线段的长EF=y2-y1,表示△PCQ与△DCQ的面积差(或△PDQ面积)
②由(2)得 ![]() .
.
∵EF=y2-y1,
∴EF=![]() ,
,
∵二次项系数小于0,
∴在![]() 范围,当
范围,当![]() 时,
时,![]() 最大.
最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图1,点D是△ABC的边BC的中点,DE⊥AC,DF⊥AB,垂足分别为E,F,且BF=CE.
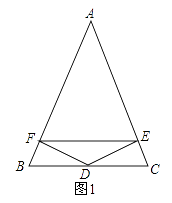
(1)求证:AE=AF;
(2)如图2,若∠BAC=60°,△ABD的面积为4,连接AD交EF于M,连接BM、CM,在不添加任何辅助线的情况下,请直接写出图中所有面积为1的三角形.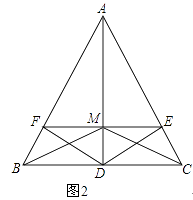
-
科目: 来源: 题型:
查看答案和解析>>【题目】x2+3x﹣4=0
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N , 再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P , 连结AP并延长交BC于点D , 则下列说法中正确的个数是( )
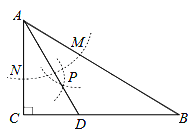
①AD是∠BAC的平分线
②∠ADC=60°
③点D在AB的垂直平分线上
④AB=2AC .
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】为发展电信事业,方便用户,电信公司对移动电话采取不同的收费方式,其中,所使用的“便民卡”与“如意卡”在某市范围内每月(30天)的通话时间x(min)与通话费y(元)的关系如图所示:
(1)分别求出通话费y1,y2与通话时间x之间的函数关系式;
(2)请帮用户计算,在一个月内使用哪一种卡便宜.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的一元二次方程x2﹣(2m﹣1)x+m2﹣m﹣2=0.
⑴不解方程,判别方程根的情况;
⑵若方程有一个根为1,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB∥CD,∠B=∠D=120°,E,F在AB上,且∠1=∠2,∠3=∠4
(1)求证:AD∥BC;
(2)求∠ACE的度数;
(3)若平行移动AD,那么∠CAF:∠CFE的值是否发生变化?若变化,找出变化规律或求出其变化范围;若不变,求出这个比值.
相关试题

