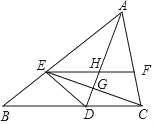
【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
参考答案:
【答案】(1)见解析;(2)50°.
【解析】
(1)根据等腰三角形三线合一的性质可得出结论;(2)由(1)可知点D为CE垂直平分线上的点,则CD=DE,∠DCE=∠DEC.由EF∥BC,可得EG平分∠DEF;由EG⊥AD,可证∠EDH=∠EHD,根据内角和定理,即可得出结论.
解:(1)∵AE=AC,AD是∠BAC平分线,
∴AD垂直平分CE;
(2)由(1)可知点D为CE垂直平分线上的点,
∴CD=DE,
∴∠DCE=∠DEC.
∵EF∥BC,
∴∠DCE=∠CEF=∠DEC,
∴EG平分∠DEF.
∵EG⊥AD,EG=EG,
∴△DEG≌△HEG(ASA),
∴△DEH是等腰三角形,且ED=EH,
∴∠EDH=∠EHD,
∵∠BCE=40°,
∴∠DEH=2∠BCE=80°,
∴∠EHD=![]() (180°﹣80°)=50°.
(180°﹣80°)=50°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于
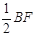 长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.
长为半径画弧,两弧交于一点P,连接AP并延长交BC于点E,连接EF.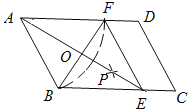
(1)四边形ABEF是_______;(选填矩形、菱形、正方形、无法确定)(直接填写结果)
(2)AE,BF相交于点O,若四边形ABEF的周长为40,BF=10,则AE的长为________,∠ABC=________°.(直接填写结果)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示的一块地,∠ADC=90°,AD=12m,CD=9m,AB=39m,BC=36m,求这块地的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)计算:
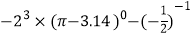
(2)化简:
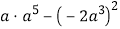
(3)化简:
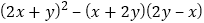
(4)化简求值:
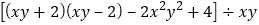 ,其中x=1009,y=
,其中x=1009,y=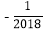
-
科目: 来源: 题型:
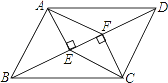
查看答案和解析>>【题目】如图,在ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=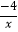 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 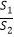 =
=  ,则b的值是 .
,则b的值是 . 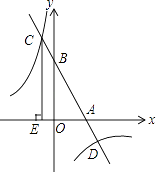
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
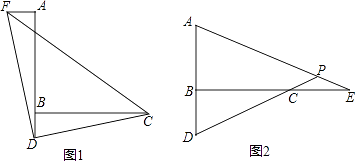
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
相关试题

