【题目】如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.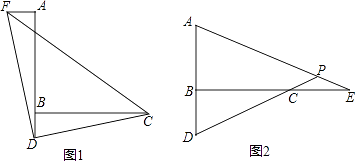
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
参考答案:
【答案】
(1)解:△CDF是等腰直角三角形,理由如下:
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
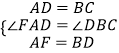 ,
,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形;
(2)解:作AF⊥AB于A,使AF=BD,连结DF,CF,如图,
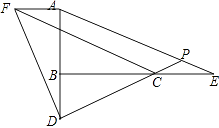
∵AF⊥AD,∠ABC=90°,
∴∠FAD=∠DBC,
在△FAD与△DBC中,
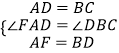 ,
,
∴△FAD≌△DBC(SAS),
∴FD=DC,
∴△CDF是等腰三角形,
∵△FAD≌△DBC,
∴∠FDA=∠DCB,
∵∠BDC+∠DCB=90°,
∴∠BDC+∠FDA=90°,
∴△CDF是等腰直角三角形,
∴∠FCD=45°,
∵AF∥CE,且AF=CE,
∴四边形AFCE是平行四边形,
∴AE∥CF,
∴∠APD=∠FCD=45°.
【解析】(1)利用SAS证出△FAD≌△DBC,再利用全等三角形的性质得出FD=DC,∠FDA=∠DCB,故△CDF是等腰直角三角形;
(2)作AF⊥AB于A,使AF=BD,连结DF,CF,如图,利用SAS证明△FAD≌△DBC,再利用全等三角形的性质得出FD=DC,![]() FDC=90°.故△CDF是等腰直角三角形,从而推出∠FCD=45°,由AF∥CE,且AF=CE,推出四边形AFCE是平行四边形,根据平行四边形的性质得出AE∥CF,根据平行线的性质得出结论。
FDC=90°.故△CDF是等腰直角三角形,从而推出∠FCD=45°,由AF∥CE,且AF=CE,推出四边形AFCE是平行四边形,根据平行四边形的性质得出AE∥CF,根据平行线的性质得出结论。
【考点精析】解答此题的关键在于理解等腰三角形的判定的相关知识,掌握如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等,以及对平行四边形的判定与性质的理解,了解若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积.
-
科目: 来源: 题型:
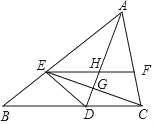
查看答案和解析>>【题目】如图,AD是∠BAC平分线,点E在AB上,且AE=AC,EF∥BC交AC于点F,AD与CE交于点G,与EF交于点H.
(1)证明:AD垂直平分CE;
(2)若∠BCE=40°,求∠EHD的度数.
-
科目: 来源: 题型:
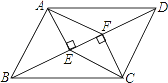
查看答案和解析>>【题目】如图,在ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断四边形AECF是不是平行四边形,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点P在一次函数y=kx+b(k,b为常数,且k<0,b>0)的图象上,将点P向左平移1个单位,再向上平移2个单位得到点Q,点Q也在该函数y=kx+b的图象上.
(1)k的值是;
(2)如图,该一次函数的图象分别与x轴、y轴交于A,B两点,且与反比例函数y=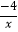 图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若
图象交于C,D两点(点C在第二象限内),过点C作CE⊥x轴于点E,记S1为四边形CEOB的面积,S2为△OAB的面积,若 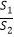 =
=  ,则b的值是 .
,则b的值是 . 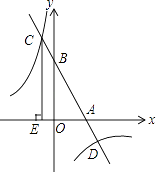
-
科目: 来源: 题型:
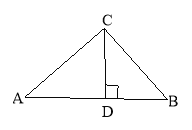
查看答案和解析>>【题目】如图,在△ABC中,CD⊥AB于点D,AC=4,BC=3,DB=
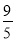 ,
,(1)求CD、AD的长
(2)判断△ABC的形状,并说明理由。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到
 .
.
(1)写出由图2所表示的数学等式:________.

(2)写出由图3所表示的数学等式:________.

(3)已知实数
 ,
, ,
, 满足
满足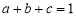 ,
, .
.①求
 的值.
的值.②求
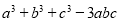 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣4,0),B(2,0),与y轴交于点C(0,2).
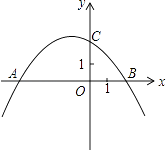
(1)求抛物线的解析式;
(2)若点D为该抛物线上的一个动点,且在直线AC上方,当以A、C、D为顶点的三角形面积最大时,求点D的坐标及此时三角形的面积;
(3)以AB为直径作⊙M,直线经过点E(﹣1,﹣5),并且与⊙M相切,求该直线的解析式.
相关试题

