搜索
【题目】如图，正方形AEFG的边AE放置在正方形ABCD的对角线AC上，EF与CD交于点M，得四边形AEMD，且两正方形的边长均为2，则两正方形重合部分（阴影部分）的面积为（ ）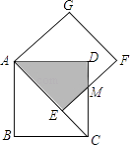 
A.﹣4+4 
B.4 +4
C.8﹣4
D. +1
参考答案：
【答案】A
【解析】解：∵四边形ABCD是正方形， ∴∠D=90°，∠ACD=45°，AD=CD=2，
则S△ACD= 
ADCD= ×2×2=2；
AC= 
AD=2 ，
则EC=2 ﹣2，
∵△MEC是等腰直角三角形，
∴S△MEC= MEEC= （2 ﹣2）2=6﹣4 ，
∴阴影部分的面积=S△ACD﹣S△MEC=2﹣（6﹣4 ）=4 ﹣4．
故选：A．
【考点精析】解答此题的关键在于理解正方形的性质的相关知识，掌握正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
-
科目： 来源： 题型：
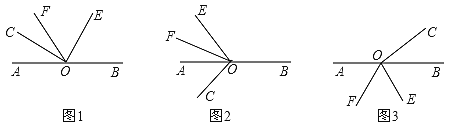
查看答案和解析>>【题目】已知O为直线AB上的一点,∠COE是直角,OF平分∠AOE(图中所说的角都是小于平角的角).
(1)如图1,若∠COF=28°,则∠BOE=______°；若∠COF=
则∠BOE=_______；∠BOE与∠COF的数量关系为_________；(2)将∠COE绕点O逆时针旋转到如图2所示的位置时,(1)中∠BOE和∠COF的数量关系否仍然成立？若成立，请说明理由？若不成立，求出∠BOE与∠COF的数量关系；
(3)当∠COE绕点O顺时针旋转到如图3的位置时,(1)中∠BOE和∠COF的数量关系是否仍然成立?若成立，请说明理由；若不成立,请求出∠BOE与∠COF的数量关系.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，⊙E的圆心E（3，0），半径为5，⊙E与y轴相交于A，B两点（点A在点B的上方），与x轴的正半轴交于点C，直线l的解析式为y=
x+4，与x轴相交于点D．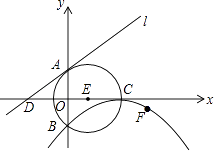
（1）求抛物线的解析式；
（2）判断直线l与⊙E的位置关系，并说明理由；
（3）动点P在抛物线上，当点P到直线l的距离最小时，求出点P的坐标及最小距离． -
科目： 来源： 题型：
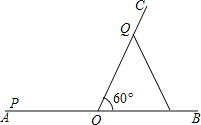
查看答案和解析>>【题目】如图，∠BOC=60°，点A是BO延长线上的一点，OA=10cm，动点P从点A出发沿AB以2cm/s的速度移动，动点Q从点O出发沿OC以1cm/s的速度移动，如果点P，Q同时出发，用t（s）表示移动的时间，当t=________s时，△POQ是等腰三角形；当t=_______s时，△POQ是直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】点A在数轴上对应的数为
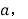点B对应的数为
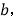且
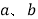满足
(1)线段AB的长为________；
(2)点C在数轴上对应的数为10,在数轴上是否存在点D,使得DA+DB=DC?若存在,求出点D对应的数；若不存在,说明理由。
(3)动点P从点A出发,以每秒6个单位长度的速度沿数轴向左均速运动；动点Q从点B出发,以每秒4个单位长度的速度沿数轴向左移动；动点M从点A出发,以每秒3个单位长度的速度沿数轴向左均速移动,点P、Q、M同时出发,设运动时间为
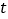秒,当
时,探究QP、QA、QM三条线段之间的数量关系,并说明理由. -
科目： 来源： 题型：
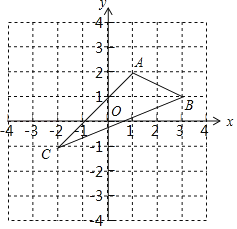
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知A（1，2），B（3，1），C（﹣2，﹣1）．
（1）在图中作出△ABC关于y轴对称的△A1B1C1．
（2）直接写出点A1，B1，C1的坐标．
A1 ， B1 ， C1 ；
（3）请你求出△A1B1C1的面积．
-
科目： 来源： 题型：
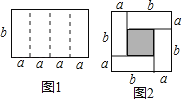
查看答案和解析>>【题目】如图1是一个长为4a、宽为b的长方形，沿图中虚线用剪刀平均分成四块小长方形，然后用四块小长方形拼成的一个“回形”正方形（如图2）．
（1）图2中阴影部分的面积为 ；
（2）观察图2，请你写出（a+b）2、（a﹣b）2、ab之间的等量关系是 ；
（3）根据（2）中的结论，若x+y=5，xy=4，求x﹣y的值．
相关试题
