搜索
【题目】南博汽车城销售某种型号的汽车，每辆进货价为25万元，市场调研表明：当销售价为29万元时，平均每周能售出8辆，而当销售价每降低0.5万元时，平均每周能多售出4辆．如果设每辆汽车降价x万元，每辆汽车的销售利润为y万元．（销售利润
销售价
进货价）
(1) 求y与x的函数关系式；在保证商家不亏本的前提下，写出x的取值范围；
(2) 假设这种汽车平均每周的销售利润为z万元，试写出z与x之间的函数关系式；
(3) 当每辆汽车的定价为多少万元时，平均每周的销售利润最大？最大利润是多少？
参考答案：
【答案】(1) y=8x+8 (0≤x≤4)(2) z=－8x2+24x+32(3) 50
【解析】
(1）
（2）
当
时，
当定价为
万元时，有最大利润，最大利润为50万元．
或：当
当定价为万元时，有最大利润，最大利润为50万元
-
科目： 来源： 题型：
查看答案和解析>>【题目】我们把形如x2=a（其中a是常数且a≥0）这样的方程叫做x的完全平方方程．
如x2=9，（3x﹣2）2=25，
…都是完全平方方程．那么如何求解完全平方方程呢？
探究思路：
我们可以利用“乘方运算”把二次方程转化为一次方程进行求解．
如：解完全平方方程x2=9的思路是：由（+3）2=9，（﹣3）2=9可得x1=3，x2=﹣3．
解决问题：
（1）解方程：（3x﹣2）2=25．
解题思路：我们只要把 3x﹣2 看成一个整体就可以利用乘方运算进一步求解方程了．
解：根据乘方运算，得3x﹣2=5 或 3x﹣2= ．
分别解这两个一元一次方程，得x1=
，x2=﹣1．（2）解方程
． -
科目： 来源： 题型：
查看答案和解析>>【题目】在一次消防演习中，消防员架起一架25米长的云梯，如图斜靠在一面墙上，梯子底端离墙7米．
（1）求这个梯子的顶端距地面有多高？
（2）如果消防员接到命令，要求梯子的顶端下降4米（云梯长度不变），那么云梯的底部在水平方向应滑动多少米？
-
科目： 来源： 题型：
查看答案和解析>>【题目】杭州休博会期间，嘉年华游乐场投资150万元引进一项大型游乐设施．若不计维修保养费用，预计开放后每月可创收33万元．而该游乐设施开放后，从第1个月到第x个月的维修保养费用累计为y（万元），且y=ax2+bx；若将创收扣除投资和维修保养费用称为游乐场的纯收益g（万元），g也是关于x的二次函数；
（1）若维修保养费用第1个月为2万元，第2个月为4万元．求y关于x的解析式；
（2）求纯收益g关于x的解析式；
（3）问设施开放几个月后，游乐场的纯收益达到最大；几个月后，能收回投资？
-
科目： 来源： 题型：
查看答案和解析>>【题目】某工厂要把一批产品从A地运往B地，若通过铁路运输，则每千米需交运费15元，还要交装卸费400元及手续费200元，若通过公路运输，则每千米需要交运费25元，还需交手续费100元（由于本厂职工装卸，不需交装卸费）.设A地到B地的路程为x km，通过铁路运输和通过公路运输需交总运费y1元和y2元，
（1）求y1和y2关于x的表达式.
（2）若A地到B地的路程为120km，哪种运输可以节省总运费？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，正方形OABC的边长为4，顶点A，C分别在x轴、y轴的正半轴上，抛物线y＝－
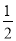x2＋bx＋c经过点B，C两点，点D为抛物线的顶点，连接AC，BD，CD.(1)求此抛物线的解析式；
(2)求此抛物线顶点D的坐标和四边形ABDC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我国从2008年6月起执行“限塑令”，“限塑令”执行前，某校为了了解本校学生所在家庭使用塑料袋的情况，随机调查了10名学生所在家庭月使用塑料袋的数量，结果如下（单位：只）：
65，70，85，75，85，79，74，91，81，95
（1）计算这10名学生所在家庭平均月使用塑料袋多少只？
（2）“限塑令”执行后，家庭平均月使用塑料袋数量预计减少
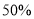，根据上面的计算后，你估计该校2000名学生所在的家庭平均月使用塑料袋一共可减少多少只？
相关试题
