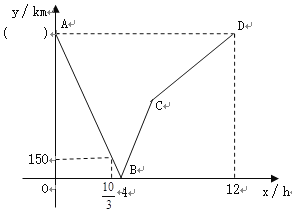
【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像回答以下问题:
(1)请在图中的( )内填上正确的值,并写出两车的速度和.
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接写出两车之间的距离不超过15km的时间范围.
参考答案:
【答案】(1)900;225km∕h.(2)yBC=225x-900(4≤x≤6);(3)![]()
【解析】试题分析:(1)设直线![]() 的解析式为:
的解析式为: ![]() 把点
把点![]() 代入,求出解析式,当
代入,求出解析式,当![]() 时,
时, ![]() 4小时后两车相遇,即可求出它们的速度和.
4小时后两车相遇,即可求出它们的速度和.
(2)由函数图象的数据,根据速度=路程÷时间就可以得出慢车的速度,由相遇问题求出速度和就可以求出快车的速度,由快车的速度求出快车走完全程的时间就可以求出点C的横坐标,由两车的距离=速度和×时间就可以求出C点的纵坐标,由待定系数法就可以求出结论.
![]() 分别让
分别让![]() 解析式中的
解析式中的![]() 即可求出两车之间的距离不超过15km的时间范围.
即可求出两车之间的距离不超过15km的时间范围.
试题解析:(1)设直线![]() 的解析式为:
的解析式为: ![]() 把点
把点![]() 代入得:
代入得:
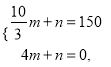
解得: ![]()
直线![]() 的解析式为:
的解析式为: ![]()
当![]() 时,
时, ![]()
图中括号里应填900,两车的速度和为: ![]()
(2)快车与慢车的速度和为:900÷4=225km/h,
慢车的速度为:900÷12=75km/h,
快车的速度为:22575=150km/h.
由题意得快车走完全程的时间为:900÷150=6h,
6时时两车之间的距离为:225×(64)=450km.
则C(6,450).
设线段BC的解析式为y=kx+b,由题意,得
![]()
解得: ![]()
则y=225x900,自变量x![]()
(3)![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,CD=6,E为BC边上一点,且EC=2将△DEC沿DE折叠,点C落在点C'.若折叠后点A,C',E恰好在同一直线上,则AD的长为( )
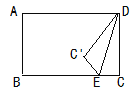
A.8B.9C.
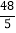 D.10
D.10 -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点O开始沿东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬行的各段路程依次为(单位:厘米):
 .问:
.问:(1)蜗牛最后是否回到出发点O?
(2)蜗牛离开出发点O最远是多少厘米?
(3)在爬行过程中,如果每爬行1厘米奖励一粒芝麻,则蜗牛可得到多少粒芝麻?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm,点P从点A出发,以每秒3cm的速度沿折线A-B-C-D方向运动,点Q从点D出发,以每秒2cm的速度沿线段DC方向向点C运动、已知动点P,Q同时出发,当点Q运动到点C时,点P,Q停止运动,设运动时间为t秒,在这个运动过程中,若△BPQ的面积为20cm2 , 则满足条件的t的值有( )
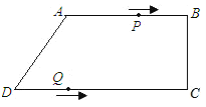
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简求值:已知:(x﹣3)2+|y+
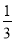 |=0,求3x2y﹣[2xy2﹣2(xy
|=0,求3x2y﹣[2xy2﹣2(xy 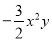 )+3xy]+5xy2的值.
)+3xy]+5xy2的值.
相关试题

