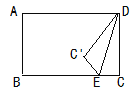
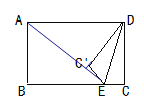
【题目】如图,矩形ABCD中,CD=6,E为BC边上一点,且EC=2将△DEC沿DE折叠,点C落在点C'.若折叠后点A,C',E恰好在同一直线上,则AD的长为( )
A.8B.9C.![]() D.10
D.10
参考答案:
【答案】D
【解析】
在Rt△DEC中,由勾股定理可得DE的长.设AD=x,则BE=x-2,AB=DC=C'D.
由Rt△AC'D≌△EBA,得到BE=AC'=x-2.在Rt△AC'D中,由勾股定理即可得出结论.
解:如图,由勾股定理得:DE=![]() .
.
设AD=x,则BE=x-2,AB=DC=C'D.
∵AD∥BE,∴∠DAE=∠AEB,∴Rt△AC'D≌△EBA(AAS),∴BE=AC'=x-2.
在Rt△AC'D中,由勾股定理得:AD2=AC'2+C'D2,即x2=(x-2)2+62,解得:x=10,即AD=10.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李师傅一家开车去旅游,出发前查看了油箱里有50升油,出发后先后走了城市路、高速路、山路最终到达旅游地点,下面的两幅图分别描述了行驶里程及耗油情况,下面的描述错误的是( )
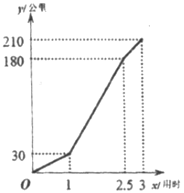
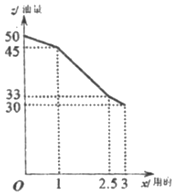
A. 此车一共行驶了210公里
B. 此车高速路一共用了12升油
C. 此车在城市路和山路的平均速度相同
D. 以此车在这三个路段的综合油耗判断50升油可以行驶约525公里
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程
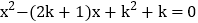 。
。(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是方程的两个实数根,第三边BC的长为5。当△ABC是等腰三角形时,求k的值。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了了解本校九年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对九年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中不近视与重度近视人数的和是中度近视人数的2倍.

请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图,在扇形统计图中,“不近视”对应扇形的圆心角度数是 144 度;
(3)若该校九年级学生有1050人,请你估计该校九年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校设计了如图所示的雕塑,取名“阶梯”, 现在工厂师傅打算用油漆喷刷所有暴露面,经测量,已知每个小立方体的棱长为0.5米.

(1)请你画出从它的正面、左面、上面三个不同方向看到的平面图形.
(2)请你帮助工人师傅计算一下,需要喷刷油漆的总面积是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某网店销售某款童装,每件售价60元,每星期可卖300件,为了促销,该网店决定降价销售.市场调查反映:每降价1元,每星期可多卖30件.已知该款童装每件成本价40元,设该款童装每件售价x元,每星期的销售量为y件.
(1)求y与x之间的函数关系式;
(2)当每件售价定为多少元时,每星期的销售利润最大,最大利润多少元?
(3)若该网店每星期想要获得不低于6480元的利润,每星期至少要销售该款童装多少件?
-
科目: 来源: 题型:
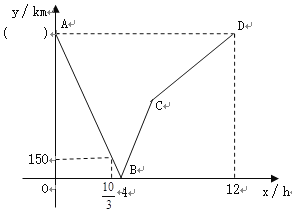
查看答案和解析>>【题目】一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系,根据图像回答以下问题:
(1)请在图中的( )内填上正确的值,并写出两车的速度和.
(2)求线段BC所表示的y与x之间的函数关系式,并写出自变量x的取值范围.
(3)请直接写出两车之间的距离不超过15km的时间范围.
相关试题

