【题目】如图,顶点为(1,4)的抛物线![]() 与直线
与直线![]() 交于点A(2,2),直线
交于点A(2,2),直线![]() 与
与![]() 轴交于点B与
轴交于点B与![]() 轴交于点C
轴交于点C
(1)求![]() 的值及抛物线的解析式
的值及抛物线的解析式
(2)P为抛物线上的点,点P关于直线AB的对称轴点在![]() 轴上,求点P的坐标
轴上,求点P的坐标
(3)点D为![]() 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
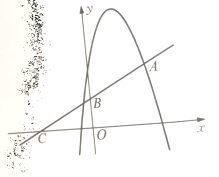
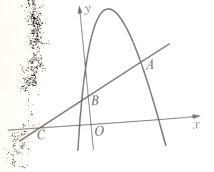
参考答案:
【答案】(1)1; ![]() ;(2)点
;(2)点![]() 的坐标(1,4)或
的坐标(1,4)或![]() ;(3)
;(3) 或
或 或
或 或
或
【解析】试题分析:(1)、将A点坐标代入一次函数解析式得出n的值,首先设二次函数的解析式为顶点式,然后将点A坐标代入得出函数解析式;(2)、如图1.设![]() 与AC的交点为H,作HM⊥x轴于M,作
与AC的交点为H,作HM⊥x轴于M,作![]() 与N,设出点P和点H的坐标,根据H是
与N,设出点P和点H的坐标,根据H是![]() 的中点得出m与x的关系式,根据相似得出x与m的关系,从而求出x的值,得出点P的坐标;(3)、设点
的中点得出m与x的关系式,根据相似得出x与m的关系,从而求出x的值,得出点P的坐标;(3)、设点![]() 坐标为A
坐标为A![]() ,以AB为边或对角线以及平行四边形的性质分别进行讨论,分别得出点的坐标.
,以AB为边或对角线以及平行四边形的性质分别进行讨论,分别得出点的坐标.
试题解析:(1)A(2,2)代入![]() 得
得![]()
设抛物线的解析式![]() 代入点)A(2,2),可得
代入点)A(2,2),可得![]()
所以抛物线的解析式![]()
(2)如图1.设![]() 与AC的交点为H,作HM⊥x轴于M,作
与AC的交点为H,作HM⊥x轴于M,作![]() 与N
与N
设![]() G
G
一方面,由于H是![]() 的中点,因此
的中点,因此![]()
于是得到所以![]() 整理,得
整理,得![]() ①
①
另一方面,由![]() 得
得![]()
所以![]() 与整理,得
与整理,得![]() ②
②
联立① ②解得![]() 或
或![]() ,所以点
,所以点![]() 的坐标(1,4)如图2)或
的坐标(1,4)如图2)或![]() (如图3)
(如图3)
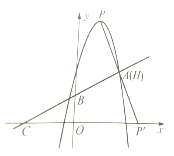
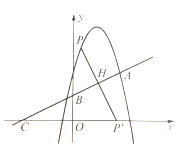

图1 图2 图3
(3)设点![]() 坐标为A
坐标为A![]() ,以AB为边或对角线进行分类讨论:
,以AB为边或对角线进行分类讨论:
①如图4,当AB是平行四边行的边时,AB//DE,AB=DE
由于点B(0,1)先向右平移2个单位,再向上平移1个单位得到A(2,2),所以点D的坐标可以表示为![]()
将![]() 代入
代入![]() ,得
,得![]()
解得![]() ,此时
,此时 如图5或
如图5或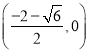 ,(如图6)
,(如图6)

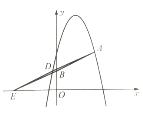
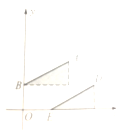
图4 图5 图6
②如图7,当AB是平行四边形的对角线时,设AB的中点![]() ,点
,点![]() E
E
关于![]() 的对称轴
的对称轴![]() 的坐标可以表示为
的坐标可以表示为![]()
将![]() 代入
代入![]() ,得
,得![]()
解得![]() ,此时
,此时 如图5)或
如图5)或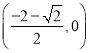 ,
,
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|m﹣2|+(n﹣1)2=0,则m+2n的值为( )
A. ﹣1 B. 4 C. 0 D. ﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,那么旋转角度的大小为( )

A.45°
B.90°
C.120°
D.135° -
科目: 来源: 题型:
查看答案和解析>>【题目】(x+a)(x﹣3)的积的常数项是15,则a的值是( )
A.12
B.5
C.-5
D.-12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果顺次连接一个四边形各边中点所得新的四边形是菱形,那么对这个四边形的形状描述最准确的是( )
A.矩形B.等腰梯形C.菱形D.对角线相等的四边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC由△A′B′C′绕O点旋转180°而得到,则下列结论不成立的是( )

A.点A与点A′是对应点
B.BO=B′O
C.∠ACB=∠C′A′B′
D.AB∥A′B′
相关试题

