【题目】如图,一块等腰直角的三角板ABC,在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,那么旋转角度的大小为( )
A.45°
B.90°
C.120°
D.135°
参考答案:
【答案】D
【解析】解:∵三角板ABC为等腰三角形,
∴∠ACB=45°,
∵在水平桌面上绕点C按顺时针方向旋转到A′B′C的位置,使A、C、B′三点共线,
∴∠A′CB′=∠ACB=45°,∠ACA′等于旋转角,
∵点A、C、B′三点共线,
∴∠ACB′=180°,
∴∠ACA′=180°﹣∠A′CB′=135°,
即旋转角为135°.
故选D.
【考点精析】解答此题的关键在于理解图形的旋转的相关知识,掌握每一个点都绕旋转中心沿相同方向转动了相同的角度,任意一对对应点与旋转中心的连线所成的角都是旋转角,对应点到旋转中心的距离相等.旋转的方向、角度、旋转中心是它的三要素,以及对旋转的性质的理解,了解①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.
-
科目: 来源: 题型:
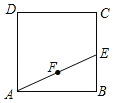
查看答案和解析>>【题目】如图,正方形ABCD的面积为3cm2,E为BC边上一点,∠BAE=30°,F为AE的中点,过点F作直线分别与AB,DC相交于点M,N.若MN=AE,则AM的长等于 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若|m﹣2|+(n﹣1)2=0,则m+2n的值为( )
A. ﹣1 B. 4 C. 0 D. ﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】将△ABC绕O点顺时针旋转50°得△A1B1C1(A、B分别对应A1、B1),则直线AB与直线A1B1的夹角(锐角)为( )
A.130°
B.50°
C.40°
D.60° -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,顶点为(1,4)的抛物线
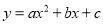 与直线
与直线 交于点A(2,2),直线
交于点A(2,2),直线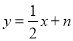 与
与 轴交于点B与
轴交于点B与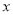 轴交于点C
轴交于点C(1)求
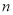 的值及抛物线的解析式
的值及抛物线的解析式(2)P为抛物线上的点,点P关于直线AB的对称轴点在
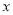 轴上,求点P的坐标
轴上,求点P的坐标(3)点D为
 轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。
轴上方抛物线上的一点,点E为轴上一点,以A 、B、E、D为顶点的四边为平行四边形时,直接写出点E的坐标。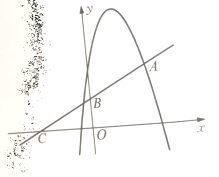
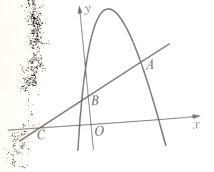
-
科目: 来源: 题型:
查看答案和解析>>【题目】(x+a)(x﹣3)的积的常数项是15,则a的值是( )
A.12
B.5
C.-5
D.-12 -
科目: 来源: 题型:
查看答案和解析>>【题目】如果顺次连接一个四边形各边中点所得新的四边形是菱形,那么对这个四边形的形状描述最准确的是( )
A.矩形B.等腰梯形C.菱形D.对角线相等的四边形
相关试题

