【题目】如图,以△ABC的一边AB为直径的半圆与其它两边AC,BC的交点分别为D,E.且![]() .
.
(1)求证:AB=AC;
(2)若AB=10,BC=12,求cos∠ABD的值.

参考答案:
【答案】(1)证明见解析(2)![]()
【解析】
试题分析:(1)先连结AE,根据ASA判定△AEB≌△AEC,再根据全等三角形的性质得出AB=AC;
(2)先根据等腰三角形的性质以及勾股定理,求得AE和BE的长,再根据面积法求得BD的长,最后计算cos∠ABD的值.
试题解析:(1)方法一:连结AE,
∵AB是直径,
∴∠AEB=∠AEC=90°,
∵![]() ,
,
∴∠BAE=∠CAE,
又AE=AE,
∴△AEB≌△AEC(ASA),
∴AB=AC;
方法二:∵AB是直径,
∴∠ADB=∠CDB=90°,
∵![]() ,
,
∴DE=BE,
∴∠CBD=∠BDE,
∴∠C=∠CDE,
∵ABED是圆内接四边形,
∴∠CDE=∠CBA,
∴∠C=∠CBA,
∴AB=AC;
(2)由(1)知△ABC为等腰三角形,AE⊥BC,
∴BE=CE=![]() BC=
BC=![]() ×12=6,
×12=6,
∵在Rt△ABE中,AB=10,BE=6,
∴AE=![]() =8,
=8,
∵AB是直径,
∴∠ADB=90°,
∴![]() ,
,
∴![]() ,
,
∴ .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四个几何体中,主视图、左视图、俯视图完全相同的是
A.圆锥B.球 C.圆柱 D.三棱柱
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣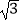 )0÷(﹣2)﹣2﹣23×2﹣2
)0÷(﹣2)﹣2﹣23×2﹣2
(2)(2x﹣1)(2x+1)﹣(x﹣6)(4x+3) -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学为调查本校学生平均每天完成作业所用时间的情况,随机调查了50名同学,如图是根据调查所得数据绘制的统计图的一部分.
请根据以上信息,解答下列问题:
(1)将统计图补充完整;
(2)若该校共有1 800名学生,根据以上调查结果估计该校全体学生平均每天完成作业所用总时间.

-
科目: 来源: 题型:
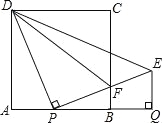
查看答案和解析>>【题目】如图,正方形ABCD的边长为1,AB边上有一动点P,连接PD,线段PD绕点P顺时针旋转90°后,得到线段PE,且PE交BC于F,连接DF,过点E作EQ⊥AB的延长线于点Q.
(1)求线段PQ的长;
(2)问:点P在何处时,△PFD∽△BFP,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】点P(2,3)向下平移2个单位,所得点的坐标是 。
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分
人数/人
70
7
80
90
1
100
8
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.
相关试题

