【题目】如图,∠CAB=∠DBA,再添加一个条件,不一定能判定△ABC≌△BAD的是( )

A. AC=BDB. ∠1=∠2C. AD=BCD. ∠C=∠D
参考答案:
【答案】C
【解析】
根据全等三角形的判定定理(SAS,ASA,AAS,SSS)判断即可.
A. ∵AC=BD,∠CAB=∠DBA,AB=AB,
∴根据SAS能推出△ABC≌△BAD,故本选项错误;
B. ∵∠CAB=∠DBA,AB=AB,∠1=∠2,
∴根据ASA能推出△ABC≌△BAD,故本选项错误;
C. 根据AD=BC和已知不能推出△ABC≌△BAD,故本选项正确;
D. ∵∠C=∠D,∠CAB=∠DBA,AB=AB,
∴根据AAS能推出△ABC≌△BAD,故本选项错误;
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在数轴上点
 表示的数分别为-2,0,6,点
表示的数分别为-2,0,6,点 与点
与点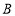 之间的距离表示为
之间的距离表示为 ,点
,点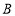 与点
与点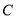 之间的距离表示为
之间的距离表示为 ,点
,点 与点
与点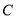 之间的距离表示为
之间的距离表示为 .
.(1)填空:
 ;
;(2)点
 开始在数轴上运动,若点
开始在数轴上运动,若点 以每秒1个单位长度的速度向左运动,同时,点
以每秒1个单位长度的速度向左运动,同时,点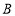 和点
和点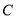 分别以每秒2个单位长度,5个单位长度的速度向右运动.
分别以每秒2个单位长度,5个单位长度的速度向右运动.①设运动时间为
 ,请用含有
,请用含有 的算式分别表示出
的算式分别表示出 ;
;②在①的条件下,
 的值是否随着时间
的值是否随着时间 的变化而变化?若变化,请说明理由;若不变,请求其值.
的变化而变化?若变化,请说明理由;若不变,请求其值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,P是等边三角形ABC内的一点,连接PA,PB,PC,以BP为边作∠PBQ=60°,且BQ=BP,连接CQ.
(1) 观察并猜想AP与CQ之间的大小关系,并证明你的结论;
(2) 若PA:PB:PC=3:4:5,连接PQ,试判断△PQC的形状,并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形ABCD中,∠DAB=∠B=∠DCB=∠D=90°,AD=BC=6,AB=CD=10.点E为射线DC上的一个动点,把△ADE沿直线AE翻折得△AD′E.

(1)当D′点落在AB边上时,∠DAE= °;
(2)如图2,当E点与C点重合时,D′C与AB交点F,
①求证:AF=FC;②求AF长.
(3)连接D′B,当∠AD′B=90°时,求DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有
 、
、 、
、 三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在∠A、∠B两内角平分线的交点处
B.在AC、BC两边垂直平分线的交点处
C.在AC、BC两边高线的交点处
D.在AC、BC两边中线的交点处
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校实验课程改革,初三年级设罝了A,B,C,D四门不同的拓展性课程(每位学生只选修其中一门,所有学生都有一门选修课程),学校摸底调査了初三学生的选课意向,并将调查结果绘制成两个不完整的统计图,问该校初三年级共有多少学生?其中要选修B、C课程的各有多少学生?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,PA⊥OA,PB⊥OB,垂足分别为A,B.下列结论中:①PA=PB;②PO平分∠APB;③OA=OB④AB垂直平分OP,一定成立的是_________(填序号)

相关试题

