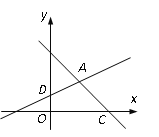
【题目】如图,在平面直角坐标系xOy中,直线y=-x+3与x轴交于点C,与直线AD交于点A(![]() ,
, ![]() ),点D的坐标为(0,1).
),点D的坐标为(0,1).
(1)求直线AD的解析式;
(2)直线AD与x 轴交于点B,若点E是直线AD上一动点(不与点B重合),当△BOD与△BCE相似时,求点E的坐标.
参考答案:
【答案】(1)求直线AD的解析式y=![]() x+1;(2)点E的坐标(2,2)或(3,
x+1;(2)点E的坐标(2,2)或(3, ![]() ).
).
【解析】试题分析:
(1) 利用点A和点D的坐标,结合一次函数的一般形式,通过待定系数法获得关于待定系数的方程,求解这些方程进而可以写出直线AD的解析式.
(2) 根据题意和相似三角形的相关知识可知,本小题应按∠BOD=∠BEC=90°和∠BOD=∠BCE=90°分为两种情况进行讨论. 在第一种情况下,可以过点E作x轴的垂线EF,利用相似三角形的关系,求得线段EC的长,进而在Rt△EFC中利用勾股定理和点E的坐标特征获得相关的方程,求解这一方程即可获得点E的坐标. 在第二种情况下,可以利用EC垂直于x轴的关系直接得到点E的横坐标值,将点E的横坐标代入直线AD的解析式即可得到点E的纵坐标值,进而写出点E的坐标.
试题解析:
(1) 设直线AD的解析式为y=kx+b (k≠0).
将点A和点D的坐标分别代入直线AD的解析式,得
 ,
,
解之,得
 ,
,
∴直线AD的解析式为![]() .
.
(2) 根据题意,分别对下面两种情况进行讨论.

①∠BOD=∠BEC=90°,即△BOD∽△BEC.
如图①,过点E作EF⊥BC,垂足为F.
设点E的坐标为(m, n).
∵点E在直线AD上,
∴![]() .
.
∴点E的坐标为(m, ![]() ).
).
∴OF=m,EF=![]() .
.
∵直线y=-x+3与x轴交于点C,
又∵当y=0时,-x+3=0,即x=3,
∴点C的坐标为(3, 0),
∴OC=3.
同理,点B的坐标为(-2, 0).
∴OB=2.
∴BC=OB+OC=2+3=5.
∵点D的坐标为(0, 1),
∴OD=1.
∴在Rt△BOD中, ![]() .
.
∵△BOD∽△BEC,
∴![]() .
.
∴![]() .
.
∵OF=m,EF=![]() .
.
∴FC=OC-OF=3-m.
∵在Rt△EFC中,EC2=EF2+FC2,
∴![]() ,
,
∴m=2.
∴![]() .
.
∴点E的坐标为(2, 2).
②∠BOD=∠BCE=90°,即△BOD∽△BCE.
设点E的坐标为(m, n).
∵∠BCE=90°,OC=3,
∴m=3.
∵点E在直线AD上,
∴当m=3时, ![]() .
.
∴点E的坐标为(3, ![]() ).
).
综上所述,点E的坐标为(2, 2)或(3, ![]() ).
).
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算(用简便方法):
(1)499×501;
(2)20202-2019×2021.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列式子(1)2x﹣7≥﹣3,(2)
 ﹣x>0,(3)7<9,(4)x2+3x>1,(5)
﹣x>0,(3)7<9,(4)x2+3x>1,(5) ﹣2(a+1)≤1,(6)m﹣n>3,中是一元一次不等式的有( )
﹣2(a+1)≤1,(6)m﹣n>3,中是一元一次不等式的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(1,0),B(0,
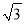 )分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.
)分别在x轴和y轴上,以线段AB为直角边在第一象限内作Rt△ABC,且使∠ABC=30°.(1)求直线AB的解析式及点C的坐标;
(2)若点P(m,
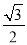 )为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
)为坐标平面内一点,使得△APB与△ABC面积相等,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】食品安全是关乎民生的重要问题,在食品中添加过量的添加剂对人体健康有害,但适量的添加剂对人体健康无害而且有利于食品的储存和运输.为提高质量,做进一步研究,某饮料加工厂需生产A、B两种饮料共100瓶,需加入同种添加剂270克,其中A饮料每瓶需加添加剂2克,B饮料每瓶需加添加剂3克,饮料加工厂生产了A、B两种饮料各多少瓶?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果代数式﹣a2+3a﹣2的值等于7,则代数式3a2﹣9a+3的值为( )
A.24
B.﹣24
C.﹣27
D.27 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各式由左边到右边的变形中,不是因式分解的是( )
A. x2-5x+6=(x-2)(x-3)
B. x2-y2+2x-2y=(x+y)(x-y)+2(x-y)
C. x(x-y)+y(y-x)=(x-y)2
D. 2x2y-3xy2=xy(2x-3y)
相关试题

