【题目】在平面直角坐标系中,O为原点,点A(3,4).

(Ⅰ)如图①,过点A作AB⊥x轴,垂足为B,则三角形AOB的面积为 ;
(Ⅱ)如图②,将点A向右平移1个单位长度,再向下平移2个单位长度,得到点A′,若P是坐标轴上的一点,要使三角形POA′的面积等于三角形OAA′的面积的4倍,则点P的坐标为 .
参考答案:
【答案】(1)6;(2)(0,10)(0,-10)(20,0)(-20,0).
【解析】
(Ⅰ)利用三角形面积公式计算可得;
(Ⅱ)先利用割补法求三角形OAA′的面积,分点P在x轴和y轴上两种情况,设其坐标,根据三角形POA′的面积等于三角形OAA′的面积的4倍列出方程求解可得.
解:(Ⅰ)△AOB的面积为![]() OBAB=
OBAB=![]() ×3×4=6,
×3×4=6,
故答案为:6;
(Ⅱ)∵点A′的坐标为(4,2),
∴三角形OAA′的面积为![]() ×(1+4)×4-
×(1+4)×4-![]() ×4×2-
×4×2-![]() ×1×2=5,
×1×2=5,
若点P在x轴上,设P(m,0),
则![]() |m|2=5×4,
|m|2=5×4,
解得:m=±20,
即P(20,0)或(-20,0);
若点P在y轴上,设(0,n),
则![]() |n|×4=5×4,
|n|×4=5×4,
解得:n=±10,
即P(0,10)或(0,-10),
故答案为:(0,10)(0,-10)(20,0)(-20,0).
-
科目: 来源: 题型:
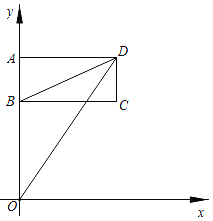
查看答案和解析>>【题目】如图,长方形ABCD在平面直角坐标系中,已知点A(0,a),B(0,6),C(b,6),且满足a=
 +8.
+8.(1)请直接写出A、C、D三个点的坐标,A ,C ,D ;
(2)连接线段BD、OD,试求三角形BOD的面积;
(3)若长方形ABCD以每秒1个单位长度匀速向下运动,设运动的时间为t秒,问是否存在某一时刻,三角形BOD的面积与长方形ABCD的面积相等?若存在,请求出t的值;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解全校学生对新闻,体育.动画、娱乐、戏曲五类电视节目的喜爱情况,机调查了100名学生,结果如扇形图所示,依据图中信息,回答下列问题:
(1)在被调查的学生中,喜欢“动画”节目的学生有 (名);
(2)在扇形统计图中,喜欢“体育”节目的学生部分所对应的扇形圆心角大小为 (度).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E、F分别是ABCD的边BC、AD上的点,且BE=DF.

(1)试判断四边形AECF的形状;
(2)若AE=BE,∠BAC=90°,求证:四边形AECF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,扇形纸扇完全打开后,阴影部分为贴纸,外侧两竹条AB,AC的夹角为120°,弧BC的长为30πcm,AD的长为15cm,则贴纸的面积等于cm2 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式(组)
(Ⅰ)解不等式5x﹣2≥3(x+1),并把它的解集在数轴上表示出来.
(Ⅱ)解不等式组

请结合题意填空,完成本题的解答.
解不等式①,得 ;
解不等式②,得 ;
把不等式①和②的解集在数轴上表示出来:

原不等式组的解集为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程、求值.
(1)解方程:x2﹣4x﹣5=0
(2)求值: sin30°+tan60°﹣cos45°+tan30°.
sin30°+tan60°﹣cos45°+tan30°.
相关试题

