【题目】某市中考体育测试有“跳绳”项目,为加强训练,某班女生分成甲、乙两组参加班级跳绳对抗赛,两组参赛人数相等,比赛结束后,依据两组学生的成绩(满分为10分)绘制了如下统计图表:
甲组学生成绩统计表
分 数 | 人 数 |
5分 | 5人 |
6分 | 2人 |
7分 | 3人 |
8分 | 1人 |
9分 | 4人 |

(1)经计算,乙组的平均成绩为7分,中位数是6分,请求出甲组学生的平均成绩、中位数,并从平均数的角度分析哪个组的成绩较好?
(2)经计算,甲组的成绩的方差是2.56,乙组的方差是多少?比较可得哪个组的成绩较为整齐?
(3)学校组织跳绳比赛,班主任决定从这次对抗赛中得分为9分的学生中抽签选取5个人组成代表队参赛,则在对抗赛中得分为9分的学生参加比赛的概率是多少?
参考答案:
【答案】
(1)
解:甲组学生的平均成绩= ![]() =6.8(分),
=6.8(分),
甲组成绩的中位数为6分,
所以从平均数的角度分析乙组的成绩较好
(2)
解:乙组的方差= ![]() [1×(5﹣7)2+7×(6﹣7)2+0×(7﹣7)2+5×(8﹣7)2+2×(9﹣7)2]≈1.71,
[1×(5﹣7)2+7×(6﹣7)2+0×(7﹣7)2+5×(8﹣7)2+2×(9﹣7)2]≈1.71,
所以甲组的方差比乙组的方差大,’
所以乙组的成绩较为整齐
(3)
解:这次对抗赛中得分为9分的学生有6人,从中抽签选取5个人组成代表队参赛,即抽签选取1个人不参赛,
所以在对抗赛中得分为9分的学生参加比赛的概率=1﹣ ![]() =
= ![]()
【解析】(1)估计平均数和中位数的定义计算甲组学生的平均成绩、中位数,然后比较平均数的大小确定哪个组的成绩较好;(2)根据方差的定义计算乙组的方差,然后根据方差的意义判断哪个组的成绩较为整齐;(3)根据概率公式求解.
【考点精析】解答此题的关键在于理解条形统计图的相关知识,掌握能清楚地表示出每个项目的具体数目,但是不能清楚地表示出各个部分在总体中所占的百分比以及事物的变化情况,以及对中位数、众数的理解,了解中位数是唯一的,仅与数据的排列位置有关,它不能充分利用所有数据;众数可能一个,也可能多个,它一定是这组数据中的数.
-
科目: 来源: 题型:
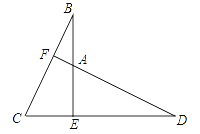
查看答案和解析>>【题目】已知:如图,BE⊥CD,BE=DE,BC=DA.
求证:(1)△BEC≌△DAE;
(2)DF⊥BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠BAC=135°,AD⊥BC于D,且AB+BD=DC,那么∠C= °.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A,B对应的数分别为-4,8.
(1)如图1,如果点P和点Q分别从点A,点B同时出发,沿数轴负方向运动,点P的运动速度为每秒2个单位,点Q的运动速度为每秒6个单位.
① 求A,B两点之间的距离.
② 当P,Q两点相遇时,点P在数轴上对应的数几.
③ 求点P出发多少秒后,与点Q之间相距4个单位长度?
(2)如图2,如果点P从点A出发沿数轴的正方向以每秒2个单位的速度运动,点Q从点B出发沿数轴的负方向以每秒6个单位的速度运动,点M从数轴原点O出发沿数轴的正方向以每秒1个单位的速度运动,若三个点同时出发,经过多少秒后有MP=MQ?


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知⊙O的直径AB=10,弦AC=6,∠BAC的平分线交⊙O于点D,过点D作DE⊥AC交AC的延长线于点E.
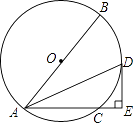
(1)求证:DE是⊙O的切线.
(2)求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个多边形的每一个内角都相等,并且每个外角都等于和它相邻的内角的一半.
(1)求这个多边形是几边形;
(2)求这个多边形的每一个内角的度数.
-
科目: 来源: 题型:
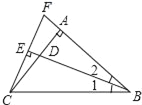
查看答案和解析>>【题目】如图所示,在△ABC中,AB=AC,∠BAC=90°,∠1=∠2,CE⊥BD交BD的延长线于点E.CE=2,延长CE,BA交于点F.
(1)求证:△ADB≌△AFC;
(2)求BD的长度.
相关试题

