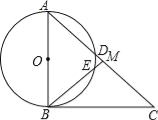
【题目】如图,在直角△ABC中,∠ABC=90°,点M是AC的中点,以AB为直径作⊙O分别交AC,BM于点D,E.
(1)求证:MD=ME;
(2)填空:连接OE,OD,当∠A的度数为 时,四边形ODME是菱形.
参考答案:
【答案】(1)证明过程见解析;(2)60°.
【解析】
试题分析:(1)、利用直角三角形斜边上的中线性质得MA=MB,则∠A=∠MBA,再利用圆内接四边形的性质证明∠MDE=∠MED,于是得到MD=ME;(2)、先证明△OAD和△OBE为等边三角形,再证明四边形DOEM为平行四边形,然后加上OD=OE可判断四边形ODME是菱形.
试题解析:(1)、在Rt△ABC中,点M是AC的中点, ∴MA=MB, ∴∠A=∠MBA;
∵四边形ABED是圆内接四边形, ∴∠ADE+∠ABE=180°, 而∠ADE+∠MDE=180°,
∴∠MDE=∠MBA; 同理可得∠MED=∠A, ∴∠MDE=∠MED, ∴MD=ME;
(2)、当∠A=60°时, 则∠ABM=60°, ∴△OAD和△OBE为等边三角形, ∴∠BOE=60°,
∴∠BOE=∠A, ∴OE∥AC, 同理可得OD∥BM, ∴四边形DOEM为平行四边形,
而OD=OE, ∴四边形ODME是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一天,小明和小玲玩纸片拼图游戏,发现利用图①中的三种材料各若干可以拼出一些长方形来解释某些等式.比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2 .
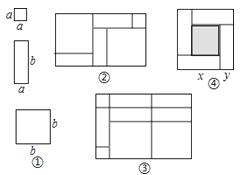
(1)图③可以解释为等式: .
(2)要拼出一个长为a+3b,宽为2a+b的长方形,需要如图所示的块,块,块.
(3)如图④,大正方形的边长为m,小正方形的边长为n,若用x、y表示四个矩形的两边长(x>y),观察图案,指出以下关系式:
(1)xy=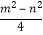 (2)x+y=m(3)x2﹣y2=mn(4)
(2)x+y=m(3)x2﹣y2=mn(4)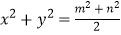
其中正确的有( )
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
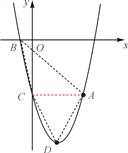
查看答案和解析>>【题目】如图,抛物线y=ax2+bx-5(a≠0)经过点A(4,-5),与x轴的负半轴交于点B,与y轴交于点C,且OC=5OB,抛物线的顶点为点D.
(1)求这条抛物线的表达式;
(2)连接AB、BC、CD、DA,求四边形ABCD的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小组的一次数学检测成绩统计如下(单位:分):76,90,64,100,84,64,73.则这组数据的众数和中位数分别是()
A.64,76B.64,100C.76,64D.64,84
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果方程x2﹣2x+m=0有两个实数根,那么m的取值范围是 .
-
科目: 来源: 题型:
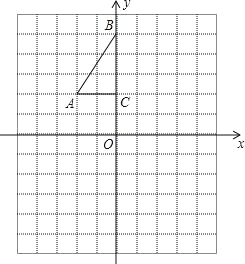
查看答案和解析>>【题目】如图,方格纸中每个小正方形的边长都是1个单位长度,Rt△ABC的三个顶点A(﹣2,2),B(0,5),C(0,2).
(1)将△ABC以点C为旋转中心旋转180°,得到△A1B1C,请画出△A1B1C的图形.
(2)平移△ABC,使点A的对应点A2坐标为(﹣2,﹣6),请画出平移后对应的△A2B2C2的图形.
(3)若将△A1B1C绕某一点旋转可得到△A2B2C2,请直接写出旋转中心的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x﹣2y=3,则代数式9﹣2x+4y的值为( )
A. ﹣3B. 3C. 6D. 12
相关试题

