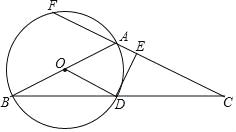
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D作⊙O的切线DE,交AC于点E,AC的反向延长线交⊙O于点F.
(1)求证:DE⊥AC;
(2)若DE+EA=8,⊙O的半径为10,求AF的长度.
参考答案:
【答案】(1)证明见解析(2)8
【解析】
试题分析:(1)欲证明DE⊥AC,只需推知OD∥AC即可;
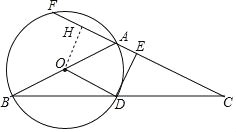
(2)如图,过点O作OH⊥AF于点H,构建矩形ODEH,设AH=x.则由矩形的性质推知:AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.在Rt△AOH中,由勾股定理知:x2+(x﹣2)2=102,通过解方程得到AH的长度,结合OH⊥AF,得到AF的值.
试题解析:(1)∵OB=OD,
∴∠ABC=∠ODB,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ODB=∠ACB,
∴OD∥AC.
∵DE是⊙O的切线,OD是半径,
∴DE⊥OD,
∴DE⊥AC;
(2)如图,过点O作OH⊥AF于点H,则∠ODE=∠DEH=∠OHE=90°,
∴四边形ODEH是矩形,
∴OD=EH,OH=DE.
设AH=x.
∵DE+AE=8,OD=10,
∴AE=10﹣x,OH=DE=8﹣(10﹣x)=x﹣2.
在Rt△AOH中,由勾股定理知:AH2+OH2=OA2,即x2+(x﹣2)2=102,
解得x1=8,x2=﹣6(不合题意,舍去).
∴AH=8.
∵OH⊥AF,
∴AH=FH=![]() AF,
AF,
∴AF=2AH=2×8=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对于二次函数y=2(x﹣1)2 +2的图象,下列说法正确的是( )
A.开口向下B.对称轴是直线x=﹣1
C.顶点坐标是(1,2)D.与x轴有两个交点.
-
科目: 来源: 题型:
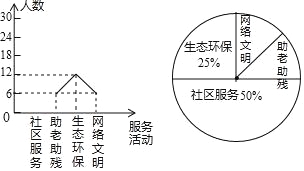
查看答案和解析>>【题目】为大力弘扬“奉献、友爱、互助、进步”的志愿服务精神,传播“奉献他人、提升自我”的志愿服务理念,东营市某中学利用周末时间开展了“助老助残、社区服务、生态环保、网络文明”四个志愿服务活动(每人只参加一个活动),九年级某班全班同学都参加了志愿服务,班长为了解志愿服务的情况,收集整理数据后,绘制以下不完整的统计图,请你根据统计图中所提供的信息解答下列问题:
(1)求该班的人数;
(2)请把折线统计图补充完整;
(3)求扇形统计图中,网络文明部分对应的圆心角的度数;
(4)小明和小丽参加了志愿服务活动,请用树状图或列表法求出他们参加同一服务活动的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣2x2y3)2﹣x3y43xy2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题正确的是( )
A.对角线互相垂直且相等的四边形是菱形
B.一组对边平行,一组邻角互补的四边形是平行四边形
C.对角线相等的四边形是矩形
D.等腰梯形的两条对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知长方形的长是(a+3b)米,宽是(a+2b)米.求它的周长和面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形有两条边分别是3和7,则这个三角形的周长是_______.
相关试题

