【题目】如图,已知数轴上原点为0,点B表示的数为2,A在B的右边,且A与B的距离为5,,动点P从点B出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时动点Q从点A出发,以每秒4个单位长度的速度向左匀速运动。设运动时间为t秒(t>0).
![]()
(1)写出数轴上点A表示的数 ,点P表示的数 (用含t的代数式表示),点Q表示的数(用含t的代数式表示);
(2)问点P与点Q何时到点O的距离相等?
(3)若点D是数轴上一点,点D表示的数是x,是否存在x,使得![]() ?如果存在,请直接写出x的值;如果不存在,说明理由.
?如果存在,请直接写出x的值;如果不存在,说明理由.
参考答案:
【答案】(1)3,-2+3t,3-4t;(2)当t=1或![]() 时,点P与点Q到点O的距离相等;(3)x的值为-3或4.
时,点P与点Q到点O的距离相等;(3)x的值为-3或4.
【解析】
(1)根据数轴的性质即可求出点A、P、Q表示的数;
(2)根据题意可分P、Q相遇前后与相遇时分别求解即可;
(3)分点D在-2左边、在-2与3之间及在3的右边分别求解即可.
(1)写出数轴上点A表示的数为-2+5=3,
点P表示的数为-2+3t,
点Q表示的数为3-4t;
(2)①P、Q相遇前后,依题意得(-2+3t)+(3-4t)=0
解得t=1,
②P、Q相遇时,依题意得(-2+3t)=(3-4t)
解得t=![]()
故当t=1或![]() 时,点P与点Q到点O的距离相等;
时,点P与点Q到点O的距离相等;
(3)①当点D在-2左边
∴![]()
解得x=-3,
②当点D在-2与3之间
∴![]() =5≠7,
=5≠7,
故无解;
③当点D在3的右边
![]()
解得x=4
综上,x的值为-3或4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,对于点P(a,b),若点P′的坐标为(a
 ,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
,ka+b)(其中k为常数,且k≠0),则称点P′为点P的“k关联点”.
(1)求点P(﹣2,3)的“2关联点”P′的坐标;
(2)若a、b为正整数,点P的“k关联点”P′的坐标为(3,6),求出k及点P的坐标;
(3)如图,点Q的坐标为(0,4 ),点A在函数y=﹣
),点A在函数y=﹣  (x<0)的图象上运动,且点A是点B的“﹣
(x<0)的图象上运动,且点A是点B的“﹣  关联点”,当线段BQ最短时,求B点坐标.
关联点”,当线段BQ最短时,求B点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD是∠ACB的平分线,∠EDC=25,∠DCE=25,∠B=70.
(1)试证明:DE∥BC;
(2)求∠BDC的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在数轴上原点为O,点P表示的数为30,点Q表示的数为120,甲、乙两只小虫分别从O,P两点出发,沿直线匀速爬向点Q,最终达到点Q.已知甲每分钟爬行60个单位长度,乙每分钟爬行30个单位长度,则在此过程中,甲、乙两只小虫相距10个单位长度时的爬行时间为_________分钟.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中有一个△ABC,顶点A(﹣1,3),B(2,0),C(﹣3,﹣1).
(1)画出△ABC关于y轴的对称轴图形△A1B1C1(不写画法);
点A1的坐标为 ;点B1的坐标为 ;点C1的坐标为 .
(2)若网格上的每个小正方形的边长为1,则△ABC的面积是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=a(x﹣h)2+k(a,h,k为常数)在坐标平面上的图象通过(0,5)、(15,8)两点.若a<0,0<h<10,则h之值可能为下列何值?( )
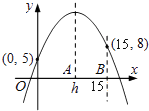
A.5
B.6
C.7
D.8 -
科目: 来源: 题型:
查看答案和解析>>【题目】新个税法于2018年9月1日全面实施,工资、薪金所得基本减除费用标准由3500元提高至5000元,并按新的税率表计算纳税:
序号
税前每月工资的各部分
税率
1
不超过5000元部分
0%
2
超过5000元至8000元的部分
3%
3
超过8000元至17000元的部分
10%
4
超过17000元至30000元的部分
20%
5
超过30000元至40000元的部分
25%
6
超过40000元至60000元的部分
30%
7
超过60000元至80000元的部分
35%
8
超过80000元的部分
45%
(1)在新个税法实施后,小王没扣税前某月工资7800元,他这个月应交税 元;
(2)在新个税法实施后,若小李没扣税前某月工资x元
 ,他这个月交税y元,则y= ;
,他这个月交税y元,则y= ;(3)在新个税法实施后,一企业某月把奖金放在工资里发放(奖金跟工资一起扣税),该企业员工小刘这个月领取了工资加奖金(税后)26410元.已知小刘没扣税前工资为a元
 ,若工资和奖金分两次发放(资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
,若工资和奖金分两次发放(资扣税,奖金不扣税),小刘这个月可以领取多少钱?(如需要,可用含a 的代数式表示)
相关试题

