【题目】已知关于x的一元二次方程x2+2x+a﹣2=0.
(1)若该方程有两个不相等的实数根,求实数a的取值范围;
(2)设方程两根为x1 , x2是否存在实数a,使 ![]() ?若存在求出实数a,若不存在,请说明理由.
?若存在求出实数a,若不存在,请说明理由.
参考答案:
【答案】
(1)解:∵b2﹣4ac=(﹣2)2﹣4×1×(a﹣2)=12﹣4a>0,
解得:a<3.
∴a的取值范围是a<3
(2)解:由根与系数的关系得:x1+x2=﹣2,x1x2=a﹣2,
又∵ ![]() ∴
∴ ![]() ,
,
有(﹣2)2﹣2(a﹣2)=1,
∴ ![]() ,
,
∵ ![]() ,
,
∴不存在实数a,使 ![]() 成立
成立
【解析】(1)根据一元二次方程有两个不相等的实数根知b2-4ac![]() 0,从而得出不等式求解即可;
0,从而得出不等式求解即可;
(2)由根与系数的关系得:x1+x2=﹣2,x1x2=a﹣2,然后将 x 1 2 + x 2 2变形成 ( x 1 + x 2 ) 2 2 x 1 x 2,然后整体代入列出关于a的方程,求出a的值,结合(1)题知a<3.从而判断这样的a不存在。
【考点精析】解答此题的关键在于理解解一元一次方程的步骤的相关知识,掌握先去分母再括号,移项变号要记牢.同类各项去合并,系数化“1”还没好.求得未知须检验,回代值等才算了,以及对求根公式的理解,了解根的判别式△=b2-4ac,这里可以分为3种情况:1、当△>0时,一元二次方程有2个不相等的实数根2、当△=0时,一元二次方程有2个相同的实数根3、当△<0时,一元二次方程没有实数根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明骑单车上学,当他骑了一段路时,想起要买某本书,于是又折回到刚经过的某书店,买到书后继续去学校.以下是他本次上学所用的时间与路程的关系示意图根据图中提供的信息回答下列问题:
(1)小明家到学校的路程是_____米,小明在书店停留了_____分钟;
(2)本次上学途中,小明一共行驶了______米,一共用了_____分钟;
(3)在整个上学的途中______(哪个时间段)小明骑车速度最快,最快的速度是____米/分;
(4)小明出发多长时间离家1200米?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的中线,点E、F在AB边上,连接DE,CF交AD于G,点E是BF中点.

(1)求证:△AFG∽△AED
(2)若FG=2,G为AD中点,求CG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°
(1)用尺规作AB的垂直平分线MN交BC于点P(不写作法,保留作图痕迹).
(2)连接AP,如果AP平分∠CAB,求∠B的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下图可以近似地刻画下列哪个情景( )
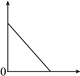
A. 小明匀速步行上学时离学校的距离与时间的关系
B. 匀速行驶的汽车的速度与时间的关系
C. 小亮妈妈到超市购买苹果的总费用与苹果质量的关系
D. 一个匀速上升的气球的高度与时间的关系
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC和△AOD是等腰直角三角形,AB=AC,AO=AD,∠BAC=∠OAD=90°,点O是△ABC内的一点,∠BOC=130°.
(1)求证:OB=DC;
(2)求∠DCO的大小;
(3)设∠AOB=α,那么当α为多少度时,△COD是等腰三角形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列证明过程.
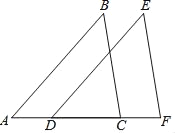
如图,已知AB∥DE,AB=DE,D,C在AF上,且AD=CF,求证:△ABC≌△DEF.
证明:∵AB∥DE
∴∠_____=∠_____(_______)
∵AD=CF
∴AD+DC=CF+DC即_____
在△ABC和△DEF中AB=DE_____
∴△ABC≌△DEF_____.
相关试题

