【题目】在平面直角坐标系xOy中,过原点O及点A(0,2)、C(6,0)作矩形OABC,∠AOC的平分线交AB于点D.点P从点O出发,以每秒 ![]() 个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.
个单位长度的速度沿射线OD方向移动;同时点Q从点O出发,以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒.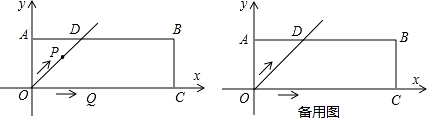
(1)当点P移动到点D时,求出此时t的值;
(2)当t为何值时,△PQB为直角三角形;
(3)已知过O、P、Q三点的抛物线解析式为y=﹣ ![]() (x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
(x﹣t)2+t(t>0).问是否存在某一时刻t,将△PQB绕某点旋转180°后,三个对应顶点恰好都落在上述抛物线上?若存在,求出t的值;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:∵四边形OABC是矩形,
∴∠AOC=∠OAB=90°,
∵OD平分∠AOC,
∴∠AOD=∠DOQ=45°,
∴在Rt△AOD中,∠ADO=45°,
∴AO=AD=2,OD=2 ![]() ,
,
∴t= ![]() =2
=2
(2)
解:要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°.
如图1,作PG⊥OC于点G,在Rt△POG中,
∵∠POQ=45°,
∴∠OPG=45°,
∵OP= ![]() t,
t,
∴OG=PG=t,
∴点P(t,t)
又∵Q(2t,0),B(6,2),
根据两点间的距离公式可得:PB2=(6﹣t)2+(2﹣t)2,QB2=(6﹣2t)2+22,PQ2=(2t﹣t)2+t2=2t2,
①若∠PQB=90°,则有PQ2+BQ2=PB2,
即:2t2+[(6﹣2t)2+22]=(6﹣t)2+(2﹣t)2,
整理得:4t2﹣8t=0,
解得:t1=0(舍去),t2=2,
∴t=2,
②若∠PBQ=90°,则有PB2+QB2=PQ2,
∴[(6﹣t)2+(2﹣t)2]+[(6﹣2t)2+22]=2t2,
整理得:t2﹣10t+20=0,
解得:t=5± ![]() .
.
∴当t=2或t=5+ ![]() 或t=5﹣
或t=5﹣ ![]() 时,△PQB为直角三角形.
时,△PQB为直角三角形.
解法2:①如图2,当∠PQB=90°时,
易知∠OPQ=90°,
∴BQ∥OD
∴∠BQC=∠POQ=45°
可得QC=BC=2,
∴OQ=4,
∴2t=4,
∴t=2,
②如图3,当∠PBQ=90°时,若点Q在OC上,
作PN⊥x轴于点N,交AB于点M,
则易证∠PBM=∠CBQ,
∴△PMB∽△QCB
∴ ![]() =
= ![]() ,
,
∴CBPM=QCMB,
∴2(t﹣2)=(2t﹣6)(6﹣t),
化简得t2﹣10t+20=0,
解得:t=5± ![]() ,
,
∴t=5﹣ ![]() ;
;
③如图4,当∠PBQ=90°时,若点Q在OC的延长线上,
作PN⊥x轴于点N,交AB延长线于点M,
则易证∠BPM=∠MBQ=∠BQC,
∴△PMB∽△QCB,
∴ ![]() =
= ![]() ,
,
∴CBPM=QCMB,
∴2(t﹣2)=(2t﹣6)(t﹣6),
化简得t2﹣10t+20=0,
解得:t=5± ![]() ,
,
∴t=5+ ![]()
(3)
解:存在这样的t值,理由如下:
将△PQB绕某点旋转180°,三个对应顶点恰好都落在抛物线上,
则旋转中心为PQ中点,此时四边形PBQB′为平行四边形.
∵PO=PQ,由P(t,t),Q(2t,0),知旋转中心坐标可表示为( ![]() t,
t, ![]() t),
t),
∵点B坐标为(6,2),
∴点B′的坐标为(3t﹣6,t﹣2),
代入y=﹣ ![]() (x﹣t)2+t,得:2t2﹣13t+18=0,
(x﹣t)2+t,得:2t2﹣13t+18=0,
解得:t1= ![]() ,t2=2
,t2=2
【解析】(1)首先根据矩形的性质求出DO的长,进而得出t的值;(2)要使△PQB为直角三角形,显然只有∠PQB=90°或∠PBQ=90°,进而利用勾股定理分别分析得出PB2=(6﹣t)2+(2﹣t)2 , QB2=(6﹣2t)2+22 , PQ2=(2t﹣t)2+t2=2t2 , 再分别就∠PQB=90°和∠PBQ=90°讨论,求出符合题意的t值即可;(3)存在这样的t值,若将△PQB绕某点旋转180°,三个对应顶点恰好都落在抛物线上,则旋转中心为PQ中点,此时四边形PBQB′为平行四边形,根据平行四边形的性质和对称性可求出t的值.
【考点精析】根据题目的已知条件,利用二次函数的性质的相关知识可以得到问题的答案,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=(x﹣3)(x+1)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,点D为顶点.

(1)求点B及点D的坐标.
(2)连结BD,CD,抛物线的对称轴与x轴交于点E.
①若线段BD上一点P,使∠DCP=∠BDE,求点P的坐标.
②若抛物线上一点M,作MN⊥CD,交直线CD于点N,使∠CMN=∠BDE,求点M的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】某学校八年级共有三个班,都参加了学校举行的书法绘画大赛,三个班根据初赛成绩分别选出了10名同学参加决赛,这些选手的决赛成绩(满分100分)如下表所示:
决赛成绩(单位:分)
八年1班
80 86 88 80 88 99 80 74 91 89
八年2班
85 85 87 97 85 76 88 77 87 88
八年3班
82 80 78 78 81 96 97 87 92 84
解答下列问题:
(1)请填写下表:
平均数(分)
众数(分)
中位数(分)
八年1班
85.5
87
八年2班
85.5
85
八年3班
78
83
(2)请从以下两个不同的角度对三个班级的决赛成绩进行
①从平均数和众数相结合看(分析哪个班级成绩好些).
②从平均数和中位数相结合看(分析哪个班级成绩好些).
(3)如果在每个班级参加决赛的选手中分别选出3人参加总决赛,你认为哪个班级的实力更强一些?请简要说明理由.
-
科目: 来源: 题型:
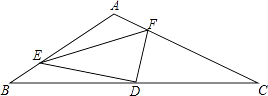
查看答案和解析>>【题目】如图,在△ABC中,∠A=120°,点D是BC的中点,点E是AB上的一点,点F是AC上的一点,∠EDF=90°,且BE=2,FC=7,则EF= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在一条直线道路上分别从相距1500米的A,B 两点同时出发,相向而行,当两人相遇后,甲继续向点B前进(甲到达点B时停止运动),乙也立即向B点返回.在整个运动过程中,甲、乙均保持匀速运动.甲、乙两人之间的距离y(米)与乙运动的时间x(秒) 之间的关系如图所示.则甲到B点时,乙距B点的距离是________米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某商店购进商品后,都加价40%作为销售价,元旦期间搞优惠促销,决定由顾客抽奖确定折扣,某顾客购买甲、乙两种商品,分别抽到七折和九折,共付款399元,商场共盈利49元,甲、乙两种商品的进价分别为多少元?
-
科目: 来源: 题型:
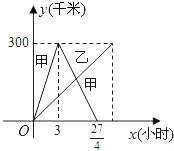
查看答案和解析>>【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)若已知乙车行驶的速度是40千米/小时,求出发后多长时间,两车离各自出发地的距离相等;
(3)在上述条件下,直接写出它们在行驶过程中相遇时的时间.
相关试题

