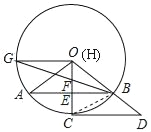
【题目】△OAB是⊙O的内接三角形,∠AOB=120°,过O作OE⊥AB于点E,交⊙O于点C,延长OB至点D,使OB=BD,连CD.
(1)求证: CD是⊙O切线;
(2)若F为OE上一点,BF的延长线交⊙O于G,连OG,![]() ,CD=6
,CD=6![]() ,求S△GOB.
,求S△GOB.

参考答案:
【答案】(1)详见解析;(2)9.
【解析】试题分析:(1)证明BC=OB=BD,可得∠OCD=90°,所以CD是⊙O切线;
(2)先求BE=3![]() ,⊙O的半径为6,过G作GH⊥OE于H,求GH的长也是6,即H与O重合,OG⊥OF,根据比例
,⊙O的半径为6,过G作GH⊥OE于H,求GH的长也是6,即H与O重合,OG⊥OF,根据比例![]() =
=![]() ,求得OF=12-6
,求得OF=12-6![]() ,最后利用面积和求面积.
,最后利用面积和求面积.
试题解析:(1)连接BC,
∵OA=OB,OE⊥AB,
∴∠AOC=∠BOC,
∵∠AOB=120°,
∴∠AOC=∠BOC=60°,
∵OC=OB,
∴BC=OB=BD,
∴CB=![]() OD,
OD,
∴∠OCD=90°,
∴CD是⊙O切线;
(2)由(1)知:∠OCD=90°,
∵∠OEB=90°,
∴AB∥CD,
∴△OEB∽△OCD,
∴![]() ,
,
∴![]() ,
,
∴BE=3![]() ,
,
Rt△OEB中,sin60°=![]() ,
,
∴OB=3![]()
![]() =6,
=6,
∴OC=6,OE=3,
过G作GH⊥OE于H,
∴GH∥BE,
∴△GHF∽△BEF,
∴![]() ,
,
∴![]() ,
,
∴GH=6,
∴GH=OG=6,
即H与O重合,OG⊥OF,
∴![]() ,
,
∵OF+EF=OE=3,
∴OF=12﹣6![]() ,
,
∴S△GOB=S△GOF+S△BOF=![]() OG
OG![]() =
=![]() (OG+BE)=
(OG+BE)=![]() (12﹣6
(12﹣6![]() )(6+3
)(6+3![]() )=9.
)=9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:关于x的方程x2﹣(2m+1)x+2m=0
(1)求证:方程一定有两个实数根;
(2)若方程的两根为x1,x2,且|x1|=|x2|,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两辆汽车分别从A、B两城同时沿高速公路驶向C城.已知A、C两城的路程为500千米,B、C两城的路程为450千米,甲车比乙车的速度快10千米/时,结果两辆车同时到达C城,求两车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:
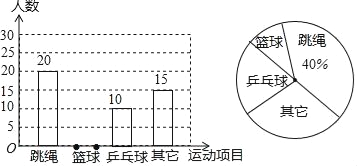
(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】将两个全等的直角三角形
 和
和 按图1方式摆放,其中
按图1方式摆放,其中  ,
, ,点
,点 落在
落在 上,
上, 所在直线交
所在直线交 所在直线于点
所在直线于点 .
.(1)求
 的度数;
的度数;(2)求证:
 ;
;(3)若将图1中
 绕点
绕点 按顺时针方向旋转至如图2,其他条件不变,请你写出如图2中
按顺时针方向旋转至如图2,其他条件不变,请你写出如图2中 与
与 之间的关系,并加以证明.
之间的关系,并加以证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x、y的二元一次方程组
 的解都为正数。
的解都为正数。(1)求a的取值范围;
(2)化简|a+1||a1|;
(3)若上述二元一次方程组的解是一个等腰三角形的一条腰和一条底边的长,且这个等腰三角形的周长为9,求a的值
-
科目: 来源: 题型:
查看答案和解析>>【题目】某乒乓球的质量检验结果如下:
抽取的乒乓球数n
50
100
200
500
1000
1500
2000
优等品的频数m
48
95
188
x
948
1426
1898
优等品的频率
 (精确到0.001)
(精确到0.001)0.960
y
0.940
0.944
z
0.951
0.949
(1)根据表中信息可得:x=______,y=______,z=______;
(2)从这批乒乓球中,任意抽取一只乒乓球是优等品的概率的估计值是多少?(精确到0.01).
相关试题

