Question

【题目】如图，抛物线y=﹣x2+3x+4与x轴交于A、B两点，与y轴交于点C，点D在抛物线上且横坐标为3．

（1）求A、B、C、D的坐标；
（2）求∠BCD的度数；
（3）求tan∠DBC的值．

Answer 1

【答案】
（1）解：令y=0，则﹣x2+3x+4=0，

即（x+1）（x﹣4）=0．

解得：x1=﹣1，x2=4．

所以A（﹣1，0），B（4，0），

令x=0，得y=4，所以C（0，4），

当x=3时，y=﹣32+3×3+4=4，

所以D（3，4）。

（2）解：∵OC=OB=4，

∴∠ABC=45°，

∵C、D的纵坐标相同，

∴CD∥AB．

又∵OC=OB，

∴∠BCD=∠OBC=45°

（3）解：过点D作DE⊥BC于点E，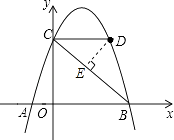

在Rt△OBC中，得BC=4 ，

在Rt△CDE中，∵CD=3，

∴CE=ED= ，

∴BE=BC﹣CE= ，

∴tan∠DBC= = ．

【解析】（1）将y=0和x=0，x=3分别代入函数解析式，求出对应的自变量的值和对应的函数值，即可求出A、B、C、D的坐标。
（2）根据点B的横坐标和点C的纵坐标相等，即可证出△OBC是等腰直角三角形，得出∠ABC=45°，再观察点C、点D的纵坐标相等得出CD∥AB，根据平行线的性质即可求出结果。
（3）添加辅助线将∠DBC转化到直角三角形中，因此过点D作DE⊥BC于点E，先根据点C和点D的坐标求出CD的长，在Rt△OBC中和在Rt△CDE中分别求出BC、DE的长，就可以求出BE的长，从而求得结果。
【考点精析】掌握抛物线与坐标轴的交点和勾股定理的概念是解答本题的根本，需要知道一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标．因此一元二次方程中的b2-4ac，在二次函数中表示图像与x轴是否有交点．当b2-4ac>0时，图像与x轴有两个交点；当b2-4ac=0时，图像与x轴有一个交点；当b2-4ac<0时，图像与x轴没有交点．；直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．